Пример 1. Выписать первые пять членов арифметической прогрессии 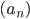 , если:
, если: 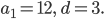
Решение.
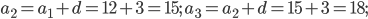
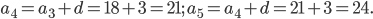
Ответ: 12; 15; 18; 21; 24.
Пример 2. Найти одиннадцатый член арифметической прогрессии 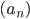 , если
, если 
Решение.

Ответ: {4}.
Пример 3. Найти семнадцатый член арифметической прогрессии 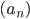 , если арифметическая прогрессия имеет вид 3; 7; 11; 15.
, если арифметическая прогрессия имеет вид 3; 7; 11; 15.
Решение.
Находим разность прогрессии:

Ответ: {67}
Пример 4. Последовательность 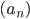 — арифметическая прогрессия.
— арифметическая прогрессия.
Найти:
a) 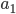 , если
, если 
б) 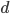 , если
, если 
Решение.
а) 
б) 
Ответ: a) {1,5}; 6) {0,8}.
Пример 5. Разность арифметической прогрессии равна 3, а сумма первых ее шести членов равна 57. Найти 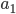 ,
,  .
.
Решение.
 Имеем
Имеем



Ответ: 
Пример 6. Найти первый член арифметической прогрессий и количество членов  , если
, если 
Решение.
Подставив данные значения из условия примера в формулы

получаем систему уравнении

Решая второе уравнение системы, получаем
 (это значение
(это значение  не подходит, т. к.
не подходит, т. к.  ).
).Итак,

Ответ:

Пример 7. Найти арифметическую прогрессию
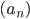 , если
, если
Решение.

Подставив в исходную систему, получаем:

Из первого уравнения системы

Подставив это значение во второе уравнение системы, получаем

Отсюда имеем равносильную исходной систему

Выпишем несколько первых членов: -2; 5; 12; 19.
Ответ:







