Пусть а ∈ N, n ∈ N. аⁿ — это степень, а — основание степени, n — показатель степени.
Степень аⁿ есть произведение n множителей, каждый из которых равен а:
![]()
Понятие степени натурального числа с натуральным показателем обобщается на степень любого действительного числа с натуральным показателем. Если а є R, n є N, то полагают по определению
![]()
Любая степень положительного числа есть положительное
число, например:
![]()
(π ≈ 3,14).
Четная степень отрицательного числа есть положительное число, например:
![]()
Нечетная степень отрицательного числа есть число отрицательное, например:
![]()
Свойства степени действительного числа с натуральным показателем
Пусть а є R, b є R, n є N, m є N. Тогда справедливы следующие свойства степени с натуральным показателем:
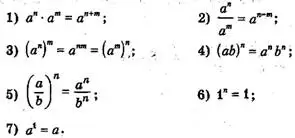
Пример 1.
![]()
Ответ: а) {32}; б) {4}; в) {36}; г) {64}.
Пример 2.
![]()
Ответ: {108}.
Пример 3.
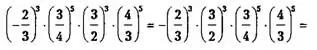
![]()
Ответ: {-1}.
Пример 4.
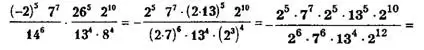
![]()
Ответ: {-364}.
Замечание 1. Формулы 1)—7) свойства степени с натуральным показателем нередко применяют в обратном порядке, т. е. справа налево. Например,
![]()
Замечание 2. В процессе решения примеров целесообразно сокращать выражения, если это возможно, так как это быстрее приводит к результату.
Пример 5.
![]()
Ответ: {54} .
Степень действительного числа с нулевым и отрицательным целым показателем
Пусть а ≠ 0, n є N. Положим по определению
![]()
Свойства 1)—6) степени с натуральным показателем справедливы и для степени действительного числа с отрицательным целым показателем. Например:
![]()
![]()
Пример 1.
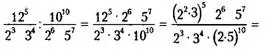
![]()
![]()
![]()
Пример 2.
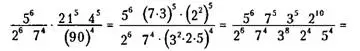
![]()






