Выделение полного квадрата двучлена из квадратного трехчлена
Пусть дан квадратный трехчлен
ах² + bх + с
и нужно преобразовать его к виду
a(x+m)² + n .
Для этого поступаем следующим образом:
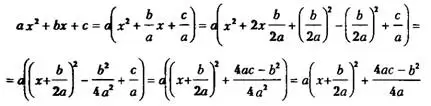
Приведем примеры на выделение полного квадрата.
Пример 1. х² - 4х + 1 = х² - 2·x·2 + 2² - 2² + 1 = (х-2)² - 4 + 1 =
= (х-2)² - 3.
Ответ: x² - 4х + 1 = (х-2)² - 3.
Пример 2.
![]()
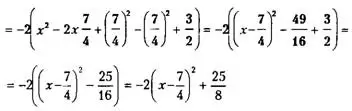
Ответ:
![]()
Разложение многочлена на множители
Разложением многочлена на множители называется преобразование многочлена в произведение двух или нескольких многочленов, среди которых могут быть и одночлены. Существует четыре основных способа разложения многочлена на множители.
Первый способ. Вынесение общего множителя за скобки.
Пример 1.
![]()
Второй способ. Способ группировки, который заключается в том, что объединяются в группы те члены, которые имеют общие множители, и выносится за скобки общий множитель каждой из групп. Если после такого преобразования окажется общий множитель у всех получившихся групп, то его выносят за скобки.
Пример 2.
![]()
![]()
(x-3y) — общий множитель.
Третий способ. Применение формул сокращенного умножения.
Пример 3.
![]()
![]()
Четвертый способ. Разложение квадратного трехчлена на линейные множители, если известны его корни. Забегая вперед, заметим, что если квадратный трехчлен ах² + bх + с имеет действительные корни x1 и х2,то он может быть разложен на линейные множители следующим образом: ах² + bх + с = a(x-x1)(x - х2).
Пример 4.
х² - Зх - 4 = (х + 1)(х - 4), так как х² - Зх - 4 = 0 <=> x1 = -1. x2 = 4 .






