Формулы сокращённого умножения — часто встречающиеся случаи умножения многочленов, используются для разложения многочленов на множители, упрощения выражений, приведения многочленов к стандартному виду. Все они доказываются непосредственным раскрытием скобок и приведением подобных слагаемых.
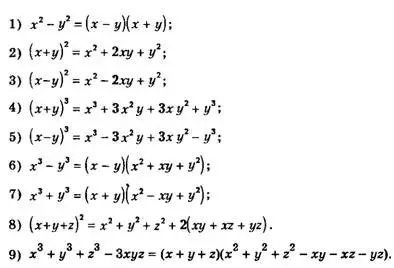
Написанные выше формулы 1)—9) применяются для преобразования (упрощения) выражений. Часто их применяют, читая не слева направо, а справа налево.
Приведем примеры на использование формул сокращенного умножения.
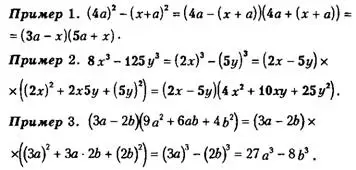
Треугольник Паскаля
Если требуется возвести двучлен в степень выше третьей, то быстрее всего это можно сделать с использованием треугольника Паскаля, который иначе называется арифметическим треугольником. Треугольник Паскаля — это числовая таблица «треугольной формы», в которой по боковым сторонам стоят единицы, а всякое другое число получается как сумма двух ближайших к нему чисел из предшествующей строки. Треугольник Паскаля имеет вид:

Треугольник Паскаля можно продолжить, заполняя элементы любой строки. Мы ограничились выписыванием семи первых строк.
Пример 1.
![]()
Пример 2.
![]()
Из примера 2 видно, что если возводится в степень разность двучлена, то наблюдается чередование знаков и после знака «+» обязательно ставится знак «-» и т. д.






