Действия над многочленами

Для того, чтобы преобразовать сумму или разность многочленов в многочлен стандартного вида, необходимо раскрыть скобки и привести подобные члены (слагаемые).

Правило раскрытия скобок

Если перед скобками стоит знак "+", то, раскрывая скобки, нужно сохранить знак каждого слагаемого суммы, заключенной в скобки. Если перед скобками стоит знак "-" то, раскрывая скобки, нужно знаки слагаемых поменять на противоположные.
Отметим следующее. Сравнивая правила грамматики с правилами математики, можно заметить, что иногда роль запятой в грамматике играет скобка в математике. Последовательность расставления запятых или скобок может иметь первостепенное
значение. Рассмотрим предложение «Казнить нельзя помиловать», в котором можно запятую расставить двумя способами: «Казнить, нельзя помиловать» и «Казнить нельзя, помиловать». Как видим, смысл совершенно противоположный и зависит от того, в каком месте поставить запятую. В математике можно рассмотреть следующие примеры:
а) (2 + 8·)5 = 10 ·5 = 50; 2 + 8· 5 = 2 + 40 = 42; 50 ≠ 42;
б) (-1)²=1; -1²=-1; 1≠-1;
в) (5-х)·х = 5·х-х²; 5-х·х = 5 - х²; 5х-х²≠5-х²;
Г) (2-ЗХ)·Х² = 2Х²-ЗХ³; 2-ЗХ·Х² = 2-ЗХ³; 2Х²-ЗХ³≠ 2-ЗХ³.
Примеры показывают, что умение правильно расставлять скобки имеет огромное значение.

Приведение подобных членов (слагаемых)

Чтобы привести подобные члены (слагаемые), достаточно сложить их числовые коэффициенты и полученное число умножить на общее буквенное выражение.
Пример.

Чтобы умножить многочлен на многочлен, надо каждый член первого многочлена умножить на каждый член второго и полученные произведения сложить. При умножении выражений нужно помнить правила знаков, а именно: (+x)·(+y) = ху; (-х)·(-у) = ху; (+х)·(-у) = -ху; (-x)·(+у) = -ху.

Деление с остатком многочлена на многочлен

Такое деление возможно, если степень многочлена, стоящего в числителе, больше или равна степени многочлена, стоящего в знаменателе. Чтобы найти частное двух многочленов, нужно расположить многочлен делимого и многочлен делителя по убывающим степеням переменной и выполнить деление.
Пусть Pm(x) и Qn(x) — многочлены степени m и n соответственно, причем m≥n :

Разделим Pm(x) и Qn(x) , получаем:

где

— многочлен степени (m-n), называемый целой частью; r(х) — многочлен степени не выше (n-1), называемый остатком. На практике деление многочленов выполняется «углом». Располагаем оба многочлена по убывающим степеням и записываем рядом, отделив «углом». Сначала делим старший член делимого на старший член делителя и записываем результат под горизонтальной чертой. Затем под делимым подписываем произведение делителя на указанный результат и вычитаем это произведение из делимого. Теперь задача свелась к делению нового многочлена меньшей степени на прежний делитель. Дальнейшие действия аналогичны описанным. В результате либо многочлен нацело разделится на многочлен (r(х) = О), либо получится остаток.
Пример 1. Разделить

Решение.

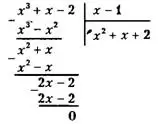
Отсюда х³ + х - 2 = (х - 1)(х² + х + 2). Таким образом, многочлен х³ + х - 2 нацело делится на многочлен (двучлен) х - 1.
Ответ:

Пример 2. Разделить

Решение.

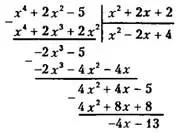
Отсюда

х² — 2x + 4 есть целая часть, а (-4x - 13) есть остаток.
Ответ: