В данном видео предлагается решение упражнений на вычисление производной показательной функции и экспоненты.
1. Найти производную функции:
а)  ;
;
б)  ;
;
в)  ;
;
г)  ;
;
д)  ;
;
е)  ;
;
ж)  ;
;
з)  ;
;
и)  .
.
2. Написать уравнение касательной к графику функции 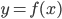 в точке с абсциссой
в точке с абсциссой  , если
, если
а)  ;
;
б)  .
.
Примеры вычисления производной показательной функции. Начала математического анализа. Видеоурок №6







