Решение систем уравнений, в которых оба уравнения содержат тригонометрические функции. Видеоурок №53

Системы уравнений, в которых оба уравнения содержат тригонометрические функции. Учимся решать задачи по тригонометрии. Видеоурок №53
Пример. Решить систему уравнений $\displaystyle \left\{\begin{matrix} \sin x \cos y=0,25,\\ \cos x\sin y=0,75. \end{matrix}\right.$
Решение. Запишем систему, равносильную исходной:
$\displaystyle \left\{\begin{matrix} \sin x\cos y+\cos x\sin y=1,\\ \sin x\cos y-\cos x\sin y=-0,5; \end{matrix}\right.$ $\displaystyle \left\{\begin{matrix} \sin (x+y)=1,\\ \sin (x-y)=-0,5, \end{matrix}\right.$ (1)
отсюда
$\displaystyle \left\{\begin{matrix} x+y=\frac{\pi }{2}+2\pi k,\, k\in \mathbb{Z},\\ x-y=(-1)^{n+1}\frac{\pi }{6}+\pi n,\, n\in \mathbb{Z}; \end{matrix}\right.$ (2)

$$\displaystyle \left[\begin{matrix} \left\{\begin{matrix} x+y=\frac{\pi }{2}+2\pi k,\\ x-y=-\frac{\pi }{6}+2\pi n, \end{matrix}\right.\\ \left\{\begin{matrix} x+y=\frac{\pi }{2}+2\pi k,\\ x-y=-\frac{5\pi }{6}+2\pi n,\, k,n\in \mathbb{Z}; \end{matrix}\right.\\ \end{matrix}\right.$$

$$\displaystyle \left[\begin{matrix} \left\{\begin{matrix} x=\frac{\pi }{6}+\pi (k+n),\\ y=\frac{\pi }{3}+\pi (k-n), \end{matrix}\right.\\ \left\{\begin{matrix} x=-\frac{\pi }{6}+\pi (k+n),\\ y=-\frac{2\pi }{3}+\pi (k-n),\, k,n\in \mathbb{Z}. \end{matrix}\right.\\ \end{matrix}\right.$$

Ответ: $\displaystyle \left ( \frac{\pi }{6}+\pi (k+n);\, \frac{\pi }{3}+\pi (k-n) \right ),\: \left ( -\frac{\pi }{6}+\pi (k+n);\, \frac{2\pi }{3}+\pi (k-n) \right ),\: k\in \mathbb{Z},\, n\in \mathbb{Z}.$
Заметим, что при переходе от системы (1) к системе (2) при записи решений первого уравнения системы мы использовали параметр 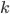$k$, а при записи решений второго уравнения — параметр $n$. Употребление только одного параметра привело бы к потере решений.

Полный урок смотрите в следующем видео:

Домашнее задание:

1. Решить систему уравнений:
1) $\displaystyle \left\{\begin{matrix} \sin x\sin y=\frac{\sqrt{3}}{4},\\ \cos x\cos y=\frac{\sqrt{3}}{4}; \end{matrix}\right.$
2) $\displaystyle \left\{\begin{matrix} \sin x\cos y=-0,5,\\ \cos x\sin y=0,5; \end{matrix}\right.$
3) $\displaystyle \left\{\begin{matrix} \cos (x-y)=2\cos (x+y),\\ \cos x\cos y=\frac{3}{4}; \end{matrix}\right.$
4) $\displaystyle \left\{\begin{matrix} \sin \pi x\cos \pi y=-\frac{1}{2},\\ \textrm{tg}\pi x \textrm{ctg}\pi y=-1. \end{matrix}\right.$
2. Решить систему уравнений:
1) $\displaystyle \left\{\begin{matrix} \sin x+\sin y=1,\\ \cos x-\cos y=\sqrt{3}; \end{matrix}\right.$
2) $\displaystyle \left\{\begin{matrix} \sin \pi x-\sin \pi y=0,5,\\ \cos \pi x-\cos \pi y=-\frac{\sqrt{3}}{2}. \end{matrix}\right.$
3. Решить систему уравнений:
1) $\displaystyle \left\{\begin{matrix} \textrm{tg}x-\textrm{tg}y=1,\\ \cos x\cos y=\frac{\sqrt{2}}{2}; \end{matrix}\right.$
2) $\displaystyle \left\{\begin{matrix} \sin ^{2}x=\cos x\cos y,\\ \cos^{2}x=\sin x \sin y. \end{matrix}\right.$