Решение задач на вычисление площадей и объемов многогранников. Геометрия. Видеоурок №1

В данном видео предлагается решение следующих задач:
1) В правильной треугольной пирамиде дана сторона основания. Она равна $a$ и двугранный угол при основании равен $\displaystyle 45^{\circ}$. Найти объем и площадь полной поверхности.
2) В прямоугольном параллелепипеде $\displaystyle ABCDA_{1}B_{1}C_{1}D_{1}$ диагональ $\displaystyle B_{1}D=13$ и известны диагонали боковых граней $\displaystyle C_{1}D=4\sqrt{10},A_{1}D=3\sqrt{17}$. Найти объем пирамиды.
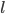3) Основанием правильной пирамиды является многоугольник, сумма внутренних углов которого $\displaystyle 720^{\circ}$. Боковое ребро пирамиды равно $l$, а угол между боковыми ребрами и высотой равен $\displaystyle 30^{\circ}$. Найти объем пирамиды.
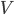4) Высота конуса $BO$ разделена на три равные части точками $\displaystyle O_{1}$ и $\displaystyle O_{2}$ и через точки деления проведены плоскости, параллельные основанию. Объем конуса равен $V$. Найти объем средней части (усеченного конуса с высотой $\displaystyle O_{1}O_{2}$).