Асимптотой кривой называется такая прямая, к которой неограниченно приближается тонка кривой при неограниченном удалении ее от начала координат.
Кривая может приближаться к своей асимптоте теми же способами, как и переменная к своему пределу: оставаясь с одной стороны от асимптоты, как, например, в задаче 1 (1) или с разных сторон, бесчисленное множество раз пересекая асимптоту и переходя с одной ее стороны на другую, как, например, в задаче 1 (3).
Для нахождения асимптот пользуются следующими положениями:
а) если при х = а кривая y = f(x) имеет бесконечный разрыв, т. е. если при 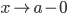 или при
или при 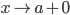 функция f(x) стремится к бесконечности (того или иного знака), то прямая х=a является ее вертикальной асимптотой;
функция f(x) стремится к бесконечности (того или иного знака), то прямая х=a является ее вертикальной асимптотой;
б) невертикальные асимптоты кривой y = f(x), если они существуют, имеют уравнения вида y=kx+b, где параметры k и b определяются формулами
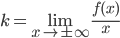 и
и ![\displaystyle b=\underset{x \to \pm \infty }{\lim }\left [ f(x)-kx \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_7563a5cda41f956ae77f66f11adf6160.gif)
при одинаковом в обеих формулах поведении х, т. е. в обеих формулах 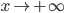 или
или 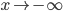 .
.
Задача 1. Найти асимптоты кривых:
1) 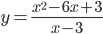 ; 2)
; 2) 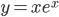 ; 3)
; 3) 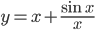 ; 4)
; 4) 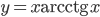 ; 5)
; 5) 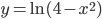 .
.
Решение.
1) (а) При х=3 данная кривая имеет бесконечный разрыв. Поэтому прямая х=3 есть ее вертикальная асимптота;
(б) далее ищем невертикальные асимптоты:

![\displaystyle b=\underset{x \to + \infty }{\lim }\left [ f(x)-kx \right ]=\underset{x \to + \infty }{\lim }\left ( \frac{x^{2}-6x+3}{x-3}-x \right )=\underset{x \to + \infty }{\lim }\frac{3-3x}{x-3}=\underset{x \to + \infty }{\lim }\frac{\frac{3}{x}-3}{1-\frac{3}{x}}=-3.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f819a5fec4d56ce3c0a1bfbc4631ca3e.gif)
Подставляя найденные значения k и b в уравнение y=kx+b, получим уравнение невертикальной асимптоты: y=x-3. Других невертикальных асимптот кривая не имеет, так как при 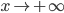 значения k и b будут те же самые. Кривая (гипербола) изображена на рис. 63.
значения k и b будут те же самые. Кривая (гипербола) изображена на рис. 63.
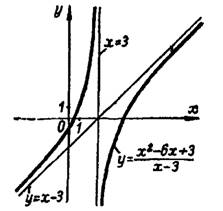
Рис.63
2) (а) Кривая не имеет вертикальных асимптот, так как она всюду непрерывна;
(б) 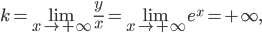
т. е. при 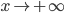 угловой коэффициент асимптоты не существует, вследствие чего при
угловой коэффициент асимптоты не существует, вследствие чего при 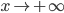 кривая не имеет асимптоты;
кривая не имеет асимптоты;
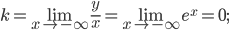
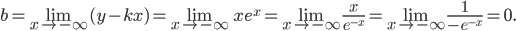
(Здесь применено правило Лопиталя.)
Следовательно, при 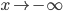 кривая имеет невертикальную асимптоту y=0 (ось Ox).
кривая имеет невертикальную асимптоту y=0 (ось Ox).
3) (а) Кривая 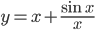 не имеет бесконечных разрывов, поэтому не имеет и вертикальных асимптот;
не имеет бесконечных разрывов, поэтому не имеет и вертикальных асимптот;
(б) 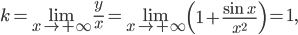 так как
так как 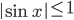 ;
;
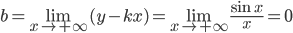 .
.
При 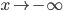 параметры асимптоты имеют те же значения. Следовательно, при
параметры асимптоты имеют те же значения. Следовательно, при 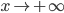 и при
и при 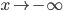 кривая имеет асимптоту у=х. Эта кривая бесчисленное множество раз пересекает свою асимптоту, переходя с одной ее стороны на другую (рис. 64).
кривая имеет асимптоту у=х. Эта кривая бесчисленное множество раз пересекает свою асимптоту, переходя с одной ее стороны на другую (рис. 64).
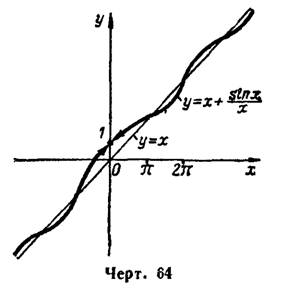
Способ приближения кривой к своей невертикальной асимптоте определяется путем исследования знака разности ординат кривой и асимптоты. Здесь эта разность 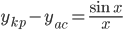 бесчисленное множество раз меняет свой знак в точках, где
бесчисленное множество раз меняет свой знак в точках, где 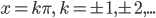 .
.
4)(а) Кривая не имеет вертикальных асимптот, так как она всюду непрерывна;
(б) 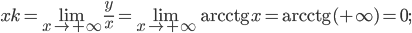
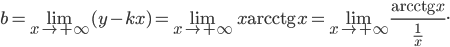
Применяя правило Лопиталя дважды, получим

Следовательно, при 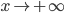 кривая имеет асимптоту у = 1:
кривая имеет асимптоту у = 1:
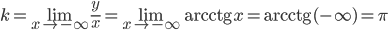 ;
;

Следовательно, при 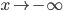 кривая имеет асимптоту
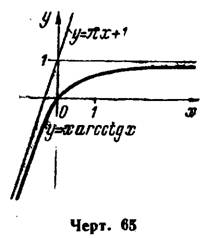
кривая имеет асимптоту 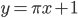 (рис. 65).
(рис. 65).
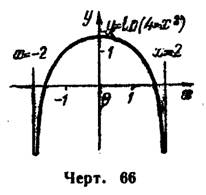
5) (а) Кривая имеет две вертикальные асимптоты х=-2 и x=2, так как при х=±2 она имеет бесконечные разрывы;
(б) невертикальных асимптот кривая не имеет, ибо ее областью расположения является интервал —2<х<2 и поэтому x не может стремиться к бесконечности (рис. 66).