Если в некотором интервале кривая расположена ниже любой своей касательной, то она называется выпуклой вверх, а если она расположена выше любой своей касательной, то называется выпуклой вниз в этом интервале.
Точкой перегиба называется точка на кривой, где меняется направление ее выпуклости.
На рис. 1 в интервале (a;b) кривая выпукла вверх, в интервале (b;c) она выпукла вниз, а точка B есть точка перегиба.
Рис.1
Направление выпуклости кривой y=f(x) характеризуется знаком второй производной y'': если в некотором интервале y''>0, то кривая выпукла вниз, а если y''<0, то кривая выпукла вверх в этом интервале.
Абсциссы точек перегиба кривой y=f(x), или графика функции f(x), являются точками, в которых меняется поведение производной y'. Поэтому их можно найти по следующему правилу:
I. Найти y'' и точки x, в которых y''=0 или не существует, а кривая непрерывна и которые лежат внутри области ее расположения.
II. Определить знак y'' слева и справа от каждой из этих точек. Исследуемая точка x будет абсциссой точки перегиба, если по разные стороны от нее y'' имеет разные знаки.
Интервалы, где кривая выпукла вверх и где она выпукла вниз, определяются из условия, что их границами могут быть только абсциссы точек перегиба, точки разрыва и граничные точки области расположения кривой.
Пример. Определить направление выпуклости и точки перегиба кривых:
1) 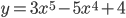 ; 2)
; 2) ![y=3-\sqrt[5]{(x+2)^{7}}](https://math-helper.ru/wp-content/plugins/latex/cache/tex_2962a174295dabcde6ed2010658bce10.gif) ;
;
3) 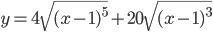 ; 4)
; 4) 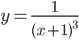 .
.
Решение. Находим точки перегиба кривой, руководствуясь указанным правилом.
1) I. Ищем точки x, в которых y''=0 или не существует, а кривая непрерывна и которые лежат внутри области расположения кривой:
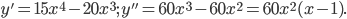
 в точках x=0 и x=1. Эти точки являются искомыми, так как область расположения и область непрерывности данной кривой есть вся ось абсцисс. Других точек x, которые могли бы быть абсциссами точек перегиба, нет, так как y'' существует всюду.
в точках x=0 и x=1. Эти точки являются искомыми, так как область расположения и область непрерывности данной кривой есть вся ось абсцисс. Других точек x, которые могли бы быть абсциссами точек перегиба, нет, так как y'' существует всюду.
II. Исследуем найденные точки, определяя знак y'' слева и справа от каждой из них. Запишем это исследование в таблицу, подобную той, которая составляется при отыскании точек экстремума:
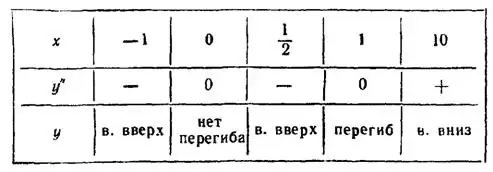
Из таблицы следует, что x=1 есть абсцисса точки перегиба кривой: y(1)=2. Поскольку эта кривая непрерывная, то во всем интервале 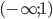 она выпукла вверх, а во всем интервале
она выпукла вверх, а во всем интервале 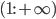 — выпукла вниз (рис. 2).
— выпукла вниз (рис. 2).
Рис.2
2) I. Находим вторую производную:
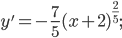
![\displaystyle y''=-\frac{14}{25}(x+2)^{-\frac{3}{5}}=-\frac{14}{25\sqrt[5]{(x+2)^{3}}}.](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f3adfa1cbf20c40793e58bf6dfae3379.gif)
Здесь y'' нигде не обращается в нуль, а при x=-2 она не существует.
При x=-2 кривая может иметь перегиб, так как ее областью расположения и областью непрерывности является вся ось абсцисс.
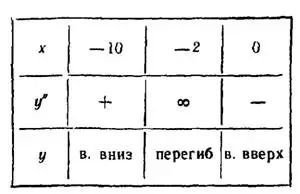
II. Исследуем значение x=-2 по знаку y'' при значениях x, меньших и больших его. Согласно таблице x=-2 есть абсцисса точки перегиба.
Слева от нее во всем интервале 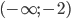 данная непрерывная кривая выпукла вниз, а справа, в интервале
данная непрерывная кривая выпукла вниз, а справа, в интервале 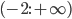 , она выпукла вверх, y(-2)=3.
, она выпукла вверх, y(-2)=3.
3) I. 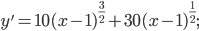
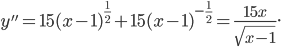
Здесь y'' обращается в нуль при x=0 и не существует (равна 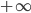 ) при x=1. Но ни одно из этих значений x не может быть абсциссой точки перегиба, так как областью расположения кривой является интервал
) при x=1. Но ни одно из этих значений x не может быть абсциссой точки перегиба, так как областью расположения кривой является интервал 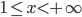 ; x=0 лежит вне этой области, а x=1 есть граница этой области, т. е. лежит не внутри ее. Кривая не имеет точек перегиба; во всей области своего расположения она выпукла вниз, так как во всей этой области y''>0.
; x=0 лежит вне этой области, а x=1 есть граница этой области, т. е. лежит не внутри ее. Кривая не имеет точек перегиба; во всей области своего расположения она выпукла вниз, так как во всей этой области y''>0.
4) 1. 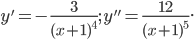
Здесь y'' не может обратиться в нуль, а при x=-1 она не существует. Однако x=-1 не может быть абсциссой точки перегиба, так как в этой точке кривая разрывна. При x<-1, y''<0; при x>-1, y''>0. Поэтому в интервале 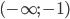 кривая выпукла вверх, а в интервале
кривая выпукла вверх, а в интервале 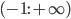 она выпукла вниз. Не имея точек перегиба, эта кривая меняет направление выпуклости при переходе x через точку разрыва x=-1.
она выпукла вниз. Не имея точек перегиба, эта кривая меняет направление выпуклости при переходе x через точку разрыва x=-1.







