Задача №1. Из куска жести, форма и размеры которого (в дм) показаны на рис. 57, вырезать прямоугольник с наибольшей площадью.
Решение. Обозначим стороны вырезаемого прямоугольника через  и
и  . Тогда его площадь
. Тогда его площадь  . Выразим
. Выразим  через
через  , исходя из подобия треугольников
, исходя из подобия треугольников  и
и  :
:

Подставляя в пропорцию
 , получим
, получим  , откуда
, откуда  . Заменяя
. Заменяя  в выражении площади, имеем
в выражении площади, имеем
где
 согласно условию задачи изменяется на отрезке [3; 11].
согласно условию задачи изменяется на отрезке [3; 11].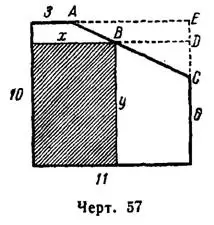
Ищем далее наибольшее значение функции
 на указанном отрезке.
на указанном отрезке.  в точке
в точке  , но эта точка лежит вне рассматриваемого отрезка;
, но эта точка лежит вне рассматриваемого отрезка;  существует всюду, поэтому на отрезке
существует всюду, поэтому на отрезке ![\left [ 3;11 \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_b17d4c830f778dac00a2120fce48107c.gif) нет ни одной критической точки. При изменении
нет ни одной критической точки. При изменении  от 3 до 11 производная , а функция
от 3 до 11 производная , а функция 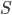 неизменно возрастает и достигает наибольшего значения на правом конце отрезка
неизменно возрастает и достигает наибольшего значения на правом конце отрезка  .
.Итак, прямоугольник, вырезанный из данного куска жести, будет иметь наибольшую площадь, когда точка
 совпадает с точкой
совпадает с точкой  ;
;  дм².
дм².Задача №2. Выбрать место для постройки моста через реку, чтобы длина дороги между двумя пунктами, расположенными по разные стороны от реки, была наименьшая.

Решение. Сделаем схематический план местности вблизи указанных в условии объектов (рис. 58). Расстояния
 и
и 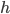 согласно условию задачи являются постоянными. Если мост построен в указанном в плане месте, то длина дороги между пунктами
согласно условию задачи являются постоянными. Если мост построен в указанном в плане месте, то длина дороги между пунктами  и
и 

Выбрав за независимую переменную
 расстояние
расстояние  , получим
, получим
и

где
 изменяется на отрезке
изменяется на отрезке ![\left [ 0;c \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f1c4357a076817f25f1e6d945c091fe6.gif) , что очевидно.
, что очевидно.Теперь найдем наименьшее значение функции
 на отрезке
на отрезке ![\left [ 0;c \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f1c4357a076817f25f1e6d945c091fe6.gif) .
.Найдем производную
 и критические точки, лежащие внутри отрезка
и критические точки, лежащие внутри отрезка ![\left [ 0;c \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f1c4357a076817f25f1e6d945c091fe6.gif) :
:
 , когда
, когда 
Решая это уравнение, получим
![x^{2}\left [ b^{2}+(x-c)^{2} \right ]=(x-c)^{2}(a^{2}+x^{2});\: b^{2}x^{2}=a^{2}(x-c)^{2};](https://math-helper.ru/wp-content/plugins/latex/cache/tex_96a32d49358f9b3386376f1902269ba6.gif)
 и
и 
Точка  лежит вне отрезка
лежит вне отрезка  : при ; при
: при ; при  . Точка
. Точка  лежит внутри этого отрезка при любых положительных значениях
лежит внутри этого отрезка при любых положительных значениях  и
и  , так как при этом и
, так как при этом и  т. е.
т. е.  .
. 
Производная  существует всюду, поэтому функция
существует всюду, поэтому функция 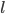 других критических точек не имеет.
других критических точек не имеет.
Внутри отрезка ![\left [ 0;c \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f1c4357a076817f25f1e6d945c091fe6.gif) функция
функция 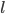 имеет одну критическую точку
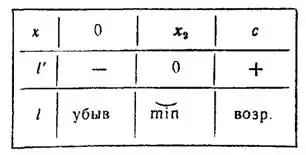
имеет одну критическую точку  . Исследуя эту критическую точку по знаку производной v слева и справа от нее, как это показано в таблице, убеждаемся, что точка
. Исследуя эту критическую точку по знаку производной v слева и справа от нее, как это показано в таблице, убеждаемся, что точка  есть точка минимума.
есть точка минимума.
Согласно свойству 1 непрерывных функций, в этой единственной на отрезке ![\left [ 0;c \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f1c4357a076817f25f1e6d945c091fe6.gif) точке минимума непрерывная функция
точке минимума непрерывная функция 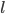 имеет и наименьшее значение из всех ее значений на этом отрезке.
имеет и наименьшее значение из всех ее значений на этом отрезке.
Следовательно, чтобы длина дороги между двумя пунктами, расположенными по разные стороны от реки, была наименьшая, следует построить мост в том месте, где расстояние  .
.







