Задачи на наибольшее (наименьшее) значения функции. Практикум по математическому анализу. Урок 55

Во многих геометрических, физических и технических задачах требуется найти наибольшее или наименьшее значение величины, связанной функциональной зависимостью с другой величиной.
Широкая распространенность и большое значение этих задач послужили одним из главных поводов к развитию математического анализа.
Для решения такой задачи следует, исходя из ее условия, выбрать независимую переменную и выразить исследуемую величину через эту переменную, а затем найти искомое наибольшее или наименьшее значение полученной функции. При этом интервал изменения независимой переменной, который может быть конечным или бесконечным, также определяется из условия задачи.

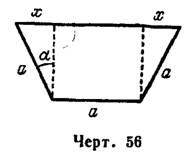
Задача 1. Из трех одинаковых тонких досок изготовить желоб с наибольшим поперечным сечением.
Решение. Поперечное сечение желоба будет представлять равнобочную трапецию (рис. 56), площадь которой $s$ зависит от наклона боковых сторон. Выберем за независимую переменную угол а между боковой стороной и высотой трапеции и выразим через эту переменную исследуемую площадь $s$:

$$x=a\sin \alpha ,\: h=a\cos \alpha ,\: s=h(a+x)$$

или

$$\displaystyle s=a^{2}(1+\sin \alpha )\cos \alpha,$$

где по смыслу задачи а может изменяться на отрезке $\displaystyle \left [ 0;\frac{\pi }{2} \right ]$. Далее найдем наибольшее значение функции $s(\alpha )$ на отрезке $\displaystyle \left [ 0;\frac{\pi }{2} \right ]$.
Найдем критические точки функции $s$, лежащие внутри этого отрезка:

$$\displaystyle s'=a^{2}\left [ \cos ^{2} \alpha -(1+\sin \alpha )\sin \alpha \right ]=a^{2}(1-\sin \alpha -2\sin ^{2}\alpha ).$$

Приравнивая производную $s'$ нулю, получим уравнение:

$$\displaystyle 2\sin ^{2}\alpha +\sin \alpha -1=0,$$

решая которое, как квадратное, найдем

$\displaystyle \sin \alpha =\frac{1}{2}$ и $\displaystyle \sin \alpha =-1$.

Из всех точек $\alpha$, определяемых этими двумя уравнениями, внутри отрезка $\displaystyle \left [ 0;\frac{\pi }{2} \right ]$ лежит только одна точка $\displaystyle \alpha =\frac{\pi }{6}$. Эта точка является критической, в ней выполняются все необходимые для этого условия. Производная $s'$ существует всюду, поэтому других критических точек нет.
Вычислим значения функции $s$ в найденной внутренней критической точке и на концах отрезка $\displaystyle \left [ 0;\frac{\pi }{2} \right ]$:

$$\displaystyle s\left ( \frac{\pi }{6} \right )=\frac{3\sqrt{3}}{4}a^{2}\approx 1,28a^{2};\: s(0)=a^{2};\: s\left ( \frac{\pi }{2} \right )=0.$$

Сравнивая эти значения, заключаем: наибольшее значение функции $s$ на отрезке $\displaystyle \left [ 0;\frac{\pi }{2} \right ]$ достигается во внутренней точке $\displaystyle \alpha =\frac{\pi }{6}$.
Таким образом, желоб из трех одинаковых досок будет иметь наибольшее поперечное сечение, когда это сечение представляет равнобочную трапецию, верхнее основание которой вдвое больше нижнего.
Задача 2. Найти размеры цилиндрической закрытой цистерны с заданным объемом $v$ и с наименьшей полной поверхностью.
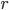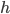Решение. Обозначив радиус и высоту цилиндра через $r$ и $h$, а его полную поверхность через $s$, получим

$$\displaystyle s=2\pi rh+2\pi r^{2}.$$

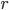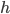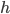Здесь переменные $r$ и $h$ не являются независимыми, а связаны между собой равенством $\displaystyle v=\pi r^{2}h$, так как согласно условию цилиндр должен иметь заданный объем $v$. Определяя из этого равенства $h$ и подставляя в выражение полной поверхности, получим

$$\displaystyle s=2\left ( \pi r^{2}+\frac{v}{r} \right ),$$

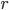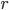где $r$ изменяется в интервале $\displaystyle 0<r<+\infty$. Выразив таким образом исследуемую полную поверхность цилиндра $s$ через одну переменную $r$, найдем теперь ее наименьшее значение при изменении 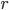$r$ в интервале $(0;+\infty )$. Найдем критические точки: $\displaystyle s'=2\left ( 2\pi r-\frac{v}{r^{2}} \right )=2\frac{2\pi r^{3}-v}{r^{2}};\: s'=0$ в единственной точке $\displaystyle r=\sqrt[3]{\frac{v}{2\pi }}$, которая лежит в рассматриваемом интервале. Эта точка является критической, так как в ней выполняются все необходимые для этого условия. Других критических точек в интервале $(0;+\infty )$ функция $s$ не имеет, так как ее производная $s'$ существует во всем этом интервале. Исследуем найденную критическую точку по знаку второй производной в этой точке:

откуда следует, что критическая точка $\displaystyle r= \sqrt[3]{\frac{v}{2\pi }}$ есть точка минимума.
Функция $s(r)$ непрерывна в интервале $(0;+\infty )$. Поэтому согласно свойству 1 непрерывных функций единственный минимум функции $s$ в интервале $(0;+\infty )$ совпадает с ее наименьшим значением в этом интервале.
При $\displaystyle r=\sqrt[3]{\frac{v}{2\pi }}$ получим $\displaystyle h=\frac{v}{\pi r^{2}}=2\sqrt[3]{\frac{v}{2\pi }}=2r$.
Следовательно, цилиндрическая закрытая цистерна, имеющая любой заданный объем, будет иметь наименьшую полную поверхность, когда ее осевое сечение представляет квадрат.