Наибольшим значением функции называется самое большее, а наименьшим значением — самое меньшее из всех ее значений.
Функция может иметь только одно наибольшее значение и только одно наименьшее значение или может не иметь их совсем. Например, во всей своей области определения функция  имеет наибольшее значение, равное единице, и наименьшее значение, равное минус единице; функции
имеет наибольшее значение, равное единице, и наименьшее значение, равное минус единице; функции  и
и  не имеют ни наибольшего, ни наименьшего значений; функция
не имеют ни наибольшего, ни наименьшего значений; функция  имеет наибольшее значение, равное нулю, но не имеет наименьшего значения; функция
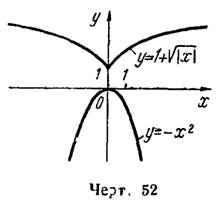
имеет наибольшее значение, равное нулю, но не имеет наименьшего значения; функция  имеет наименьшее значение, равное единице, но не имеет наибольшего значения (рис. 52).
имеет наименьшее значение, равное единице, но не имеет наибольшего значения (рис. 52).
Нахождение наибольшего и наименьшего значений непрерывных функций основывается на следующих свойствах этих функций:
1) Если в некотором интервале (конечном или бесконечном) функция  непрерывна и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале.
непрерывна и имеет только один экстремум и если это максимум (минимум), то он будет наибольшим (наименьшим) значением функции в этом интервале.
2) Если функция  непрерывна на некотором отрезке
непрерывна на некотором отрезке ![\left [ a,b \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_77c4ded661666dc920e508d89d5a97cf.gif) , то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри отрезка, или на границах этого отрезка.
, то она обязательно имеет на этом отрезке наибольшее и наименьшее значения. Эти значения достигаются ею или в точках экстремума, лежащих внутри отрезка, или на границах этого отрезка.
Отсюда вытекает практическое правило для нахождения наибольшего или наименьшего значения функции  на отрезке
на отрезке ![\left [ a,b \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_77c4ded661666dc920e508d89d5a97cf.gif) , где она непрерывна:
, где она непрерывна:
I. Найти критические точки, лежащие внутри отрезка ![\left [ a,b \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_77c4ded661666dc920e508d89d5a97cf.gif) , и вычислить значения функции в этих точках (не вдаваясь в исследование, будет ли в них экстремум функции и какого вида).
, и вычислить значения функции в этих точках (не вдаваясь в исследование, будет ли в них экстремум функции и какого вида).
II. Вычислить значения функций на концах отрезка, т. е.  и
и  .
.
III. Сравнить полученные значения функции: самое большее из них будет наибольшим значением, а самое меньшее — наименьшим значением функции на всем данном отрезке.
Пример 1. Найти наибольшее и наименьшее значения каждой из следующих функций:
1)  на отрезке
на отрезке ![\left [ -4,4 \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_c9c96fc059be9d780f9735523bbb7562.gif) ;
;
2)  на отрезке
на отрезке ![\left [ 1,e \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_ee7962eb8393aea22d8c5a1fe94157da.gif) ;
;
3)  на отрезке
на отрезке ![\left [ 0;\frac{3}{2}\pi \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_da0cca5563fd98372d3ef615350d3596.gif) ;
;
4)  .
.
Решение. Согласно практическому правилу:
1) I. Найдем критические точки функции  , лежащие внутри отрезка
, лежащие внутри отрезка ![\left [ -4,4 \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_c9c96fc059be9d780f9735523bbb7562.gif) , и вычислим ее значения в этих точках:
, и вычислим ее значения в этих точках:  в точках
в точках 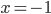 и
и 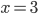 . Эти точки лежат внутри отрезка
. Эти точки лежат внутри отрезка ![\left [ -4,4 \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_c9c96fc059be9d780f9735523bbb7562.gif) и являются критическими. Других критических точек нет, так как производная
и являются критическими. Других критических точек нет, так как производная  существует всюду. Значения функций и в критических точках:
существует всюду. Значения функций и в критических точках:  .
.
II. Вычислим значения функции на концах отрезка ![\left [ -4,4 \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_c9c96fc059be9d780f9735523bbb7562.gif) :
:  .
.
III. Сравнивая все вычисленные значения функции во внутренних критических точках и на концах отрезка, заключаем: наибольшее значение функции  на отрезке
на отрезке ![\left [ -4,4 \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_c9c96fc059be9d780f9735523bbb7562.gif) равно 40 и достигается ею во внутренней критической точке
равно 40 и достигается ею во внутренней критической точке 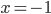 , а ее наименьшее значение равно -41 и достигается на левой границе отрезка
, а ее наименьшее значение равно -41 и достигается на левой границе отрезка  (рис.53).
(рис.53).
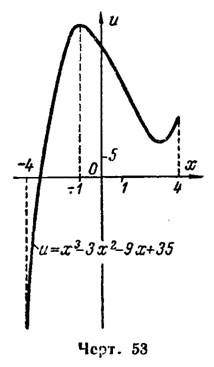
2) I. Ищем критические точки:  в точках
в точках  и
и  . Точка
. Точка  лежит вне области определения данной функции
лежит вне области определения данной функции 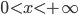 ; точка
; точка  лежит вне заданного отрезка
лежит вне заданного отрезка ![\left [ 1;e \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_1a67709a5aa5f924ef4d57c072ab2819.gif) . Производная
. Производная  существует во всем интервале определения функции
существует во всем интервале определения функции  . Поэтому внутри заданного отрезка нет критических точек.
. Поэтому внутри заданного отрезка нет критических точек.
II. Вычислим значения функции  на концах отрезка:
на концах отрезка:  .
.
III. Поскольку внутри отрезка ![\left [ 1;e \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_1a67709a5aa5f924ef4d57c072ab2819.gif) нет критических точек, то функция изменяется на этом отрезке монотонно и ее наименьшее и наибольшее значения на этом отрезке достигаются на концах отрезка:
нет критических точек, то функция изменяется на этом отрезке монотонно и ее наименьшее и наибольшее значения на этом отрезке достигаются на концах отрезка:  (рис. 54).
(рис. 54).
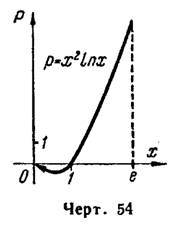
3) I. Найдем критические точки:  при
при  и
и  ; корни первого уравнения
; корни первого уравнения  , корни второго уравнения
, корни второго уравнения  , где
, где  .
.
Из них внутри заданного отрезка ![\displaystyle \left [ 0;\frac{3}{2}\pi \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_3ec2d7a5e2919c8e4fc0bcff0327ff7b.gif) лежат критические точки
лежат критические точки  и
и  . Производная
. Производная  существует всюду, поэтому других критических точек функция
существует всюду, поэтому других критических точек функция 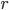 не имеет. Значения функции в найденных внутренних критических точках
не имеет. Значения функции в найденных внутренних критических точках  и
и  :
:
 .
.
II. Вычислим значения функции на концах отрезка:  .
.
III. Сравнение вычисленных значений функции во внутренних критических точках и на концах отрезка показывает, что ее наибольшее значение на этом отрезке  ,
,
наименьшее значение  .
.
4) Здесь изменение аргумента  не ограничено каким-либо отрезком, а функция определена на всей числовой оси. Поэтому следует рассмотреть все значения функции, принимаемые ею при изменении
не ограничено каким-либо отрезком, а функция определена на всей числовой оси. Поэтому следует рассмотреть все значения функции, принимаемые ею при изменении  от
от  до
до  .
.
I. Найдем критические точки:  в точке
в точке  .
.
Эта точка является критической, так как функция всюду определена и непрерывна. Других критических точек нет, так как производная  существует всюду.
существует всюду.
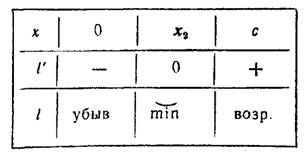
II. Исследуем критическую точку  по знаку первой производной слева и справа от этой точки (см. табл.). Это исследование показывает, что точка
по знаку первой производной слева и справа от этой точки (см. табл.). Это исследование показывает, что точка  есть точка минимума, где
есть точка минимума, где  .
.
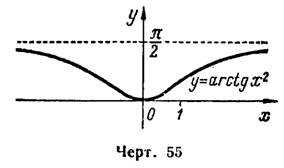
III. Основываясь на указанном выше свойстве 1 непрерывных функций, заключаем: функция  , как имеющая единственный экстремум — минимум и не имеющая точек разрыва, имеет наименьшее значение, совпадающее с ее минимумом,
, как имеющая единственный экстремум — минимум и не имеющая точек разрыва, имеет наименьшее значение, совпадающее с ее минимумом,

но не имеет наибольшего значения, хотя она не растет неограниченно. При
 она асимптотически приближается к значению — (рис. 55).
она асимптотически приближается к значению — (рис. 55).






