Общая схема исследования функций и построения их графиков. Практикум по математическому анализу. Урок 59

Общее исследование функций и построение их графиков удобно выполнять по следующей схеме:
I. Найти область определения функции.
II. Найти точки разрыва функции и ее односторонние пределы в этих точках.
III. Выяснить, не является ли функция четной, нечетной или периодической.
IV. Найти; точки пересечения графика функции с осями координат и интервалы знакопостоянства функции.
V. Найти асимптоты графика функции: а) вертикальные и б) не-вертикальные.
VI. Найти точки экстремума и интервалы возрастания и убывания функции.
VII. Найти точки перегиба графика функции и интервалы его выпуклости вверх и вниз.
VIII. Построить график функции, используя все полученные результаты исследования. Если их окажется недостаточно, то следует найти еще несколько точек графика функции, исходя из ее уравнения. Построение графика функции целесообразно выполнять по его элементам, вслед за выполнением "отдельных пунктов исследования.
Задача 1. Исследовать функцию 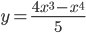$\displaystyle y=\frac{4x^{3}-x^{4}}{5}$ и построить ее график.
Решение. Руководствуясь указанной общей схемой, последовательно находим:
1) I. Областью определения данной функции, как и всякого многочлена, является вся числовая ось.
II. Функция не имеет точек разрыва. Как у всякой элементарной функции, ее область непрерывности совпадает с областью определения.
III. Функция не является ни четной, ни нечетной, ни периодической.
IV. При х = 0 из данного уравнения найдем y=0, а при у = 0 найдем х = 0 и х = 4. Это значит, что график функции пересекает координатные оси в точках (0; 0) и (4; 0).
Интервалы, на которых функция сохраняет знак, определяются из условия, что их границами могут быть только точки пересечения графика функции с осью Ох, точки разрыва и границы области определения функции.
Для исследуемой функции такими точками являются точки х = 0 и х = 4. Определяя знак функции при каком-либо значении х из интервала 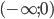$(-\infty ;0)$, например у(- 1)<0, заключаем, что во всем этом интервале функция имеет отрицательные значения; во всем интервале (0; 4) функция имеет положительные значения, ибо y(1)>0; во всем интервале 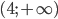$(4;+\infty)$ функция имеет отрицательные значения, так как у(10)<0.
V. а) Вертикальных асимптот график функции не имеет, так как она всюду непрерывна;
б)

$\displaystyle k=\underset{x \to +\infty}{\lim }\frac{y}{x}=\frac{1}{5}\underset{x \to +\infty}{\lim }x^{2}(4-x)=-\infty.$

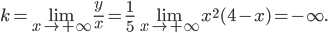
При 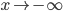$x \to -\infty$ угловой коэффициент k асимптоты также не существует. Поэтому невертикальных асимптот график функции также не имеет.
VI. 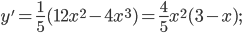$\displaystyle y'=\frac{1}{5}(12x^{2}-4x^{3})=\frac{4}{5}x^{2}(3-x);$
y' = 0 в точках х = 0 и x = 3, которые являются критическими, так как они удовлетворяют всем необходимым для этого условиям. Других критических точек нет, поскольку производная у' существует всюду.
Исследуем критические точки по знаку у' слева и справа от каждой из этих точек:

Следовательно, х = 3 есть точка максимума: 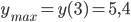$y_{max}=y(3)=5,4$.
Интервалы возрастания и убывания функции определяются из условия, что их границами могут быть только точки экстремума, точки разрыва и границы области определения функции.
Исследуемая функция всюду непрерывна и имеет единственную точку максимума x = 3. Поэтому в интервале 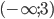$(-\infty;3)$ она возрастает, а в интервале 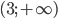$(3;+\infty)$ — убывает.
VII. 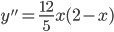$\displaystyle y''=\frac{12}{5}x(2-x)$ всюду существует и обращается в нуль
при x = 0 и х = 2. Эти значения х могут быть абсциссами точек перегиба. Исследуем их, определяя знак у" слева и справа:

Следовательно, график функции имеет две точки перегиба (0; 0) и (2; 3,2) (их ординаты найдены из данного уравнения).

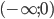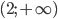Так как исследуемая функция непрерывна на всей числовой оси, то, согласно таблице, в интервалах $(-\infty;0)$ и $(2;+\infty)$ ее график обращен выпуклостью вверх, а в интервале (0; 2) он обращен выпуклостью вниз.
VIII. Учитывая все полученные результаты исследования-строим график функции (рис. 68).