Двойное векторное произведение трех векторов

Двойным векторным или векторно-векторным произведением трех векторов 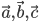$\vec{a},\vec{b},\vec{c}$ называется выражение вида
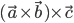$(\vec{a}\times \vec{b})\times \vec{c}$ или $\vec{a}\times (\vec{b}\times \vec{c}).$
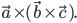
Для двойного векторного произведения 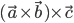$(\vec{a}\times \vec{b})\times \vec{c}$ надо сначала умножить векторно два вектора $\vec{a}$ и $\vec{b}$, а затем полученное произведение еще раз умножают векторно на третий вектор $\vec{c}$.
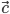Двойное векторное произведение выражается формулами

$$(\vec{a}\times \vec{b})\times \vec{c}=\vec{b}\left(\vec{a}\vec{c} \right)-\vec{a}\left(\vec{b}\vec{c} \right),$$

$$\vec{a}\times (\vec{b}\times \vec{c})=\vec{b}\left(\vec{a} \vec{c}\right)-\vec{c}\left(\vec{a} \vec{b}\right)\; \; \left(1 \right)$$

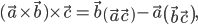
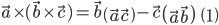
Правило: Двойное векторное произведение равно произведению среднего вектора на скалярное произведение двух других, минус крайний вектор в скобке, умноженный на скалярное произведение двух других.
Если векторы 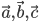$\vec{a},\vec{b},\vec{c}$ заданы своими проекциями

$$\vec{a}=x_{1}\vec{i}+y_{1}\vec{j}+z_{1}\vec{k},\; \vec{b}=x_{2}\vec{i}+y_{2}\vec{j}+z_{2}\vec{k},\;\vec{c}=x_{3}\vec{i}+y_{3}\vec{j}+z_{3}\vec{k},\;$$

то двойное векторное произведение $\vec{a}\times (\vec{b}\times \vec{c})$ будет равно:

$$\vec{a}\times (\vec{b}\times \vec{c})=\begin{vmatrix} \vec{i} & \vec{j} &\vec{k} \\ x_{1} & y_{1} &z_{1} \\ \begin{vmatrix} y_{2} & z_{2}\\ y_{3}& z_{3} \end{vmatrix}&\begin{vmatrix} z_{2} &x_{2} \\ z_{3}& x_{3} \end{vmatrix} & \begin{vmatrix} x_{2} & y_{2}\\ x_{3}& y_{3} \end{vmatrix} \end{vmatrix}=$$

$$=(y_{1}(x_{2}y_{3}-x_{3}y_{2})-z_{1}(x_{3}z_{2}-x_{2}z_{3}))\vec{i}+$$

$$+(z_{1}(y_{2}z_{3}-y_{3}z_{2})-x_{1}(x_{2}y_{3}-x_{3}y_{2}))\vec{j}+$$

$$+(x_{1}(x_{3}z_{2}-x_{2}z_{3})-y_{1}(y_{2}z_{3}-y_{3}z_{2}))\vec{k}.$$