Линейные операции над векторами. Примеры решения задач. Часть 1

Задача № 1. По данным векторам $\vec{a}$ и $\vec{b}$ построить каждый из следующих векторов:
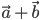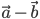1) $\vec{a}+\vec{b}$ ; 2) $\vec{a}-\vec{b}$ .
Пусть даны такие два вектора $\vec{a}$ и $\vec{b}$ .
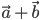1) $\vec{a}+\vec{b}$ .
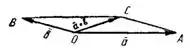
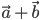I способ. Помещаем начало векторов $\vec{a}$ и $\vec{b}$ в точку О и строим параллелограмм ОВСА. Диагональ ОС изображает сумму $\vec{a}+\vec{b}$ .

Рис.1

Рис.2

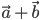II способ. Помещаем начало вектора $\vec{a}$ в точку О, начало вектора $\vec{b}$ совмещаем с концом вектора $\vec{a}$ . Замыкающий вектор есть $\vec{a}+\vec{b}$ . Его начало — в точке О, а конец совпадает с концом вектора $\vec{b}$ .

Рис.3

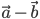2) $\vec{a}-\vec{b}$ .
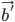I способ. Начало вектора $\vec{a}$ помещаем в точку О и строим вектор $\vec{b'}$ по длине равный вектору $\vec{b}$ , но противоположного направления.

Рис.4

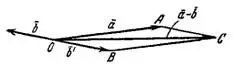
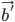Теперь находим сумму векторов $\vec{a}$ и $\vec{b'}$ по правилу параллелограмма. Искомый вектор $\vec{OC}=\vec{a}-\vec{b}$ .
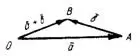
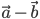II способ. Начало векторов $\vec{a}$ и $\vec{b}$ помещаем в одну точку О. Концы векторов соединяем. Замыкающий вектор есть $\vec{a}-\vec{b}$ ; его начало — в конце вектора $\vec{b}$ , конец — в конце вектора $\vec{a}$ .

Рис.5

Задача № 2. В треугольнике ABC вектор 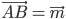$\vec{AB}=\vec{m}$ и вектор 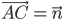$\vec{AC}=\vec{n}$ . Построить каждый из следующих векторов:
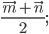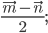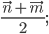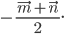
1) $\frac{\vec{m}+\vec{n}}{2};$ 2) $\frac{\vec{m}-\vec{n}}{2};$ 3) $\frac{\vec{n}+\vec{m}}{2};$ 4) $-\frac{\vec{m}+\vec{n}}{2}.\;$
Решение задачи №2 подробно изложено в следующем видео

Задача № 3. Точка О является центром тяжести треугольника ABC. Доказать, что 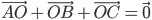$\vec{AO}+\vec{OB}+\vec{OC}=\vec{0}$ .
Задача № 4. В правильном пятиугольнике ABCDE заданы векторы, совпадающие с его сторонами: 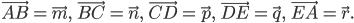$\vec{AB}=\vec{m},\; \vec{BC}=\vec{n},\; \vec{CD}=\vec{p},\; \vec{DE}=\vec{q}, \; \vec{EA}=\vec{r}.$
Построить вектор:
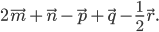
$2\vec{m}+\vec{n}-\vec{p}+\vec{q}-\frac{1}{2}\vec{r}.$
Решения этих задач подробно изложено в следующем видео