Задача № 1.
Даны: 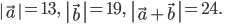
Вычислить 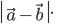 .
.
Решение. Предположим, что нам даны векторы  и
и  . Найдем векторы
. Найдем векторы 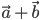 и
и 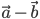 . Вектор
. Вектор 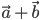 есть одна из диагоналей параллелограмма, построенного на векторах
есть одна из диагоналей параллелограмма, построенного на векторах  и
и  , вектор
, вектор 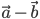 — вторая его диагональ (рис.1).
— вторая его диагональ (рис.1).
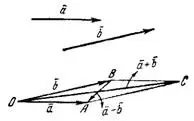
Рис.1
Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон.

откуда



Ответ:

Задача № 2. В параллелепипеде ABCDA₁B₁C₁D₁ заданы векторы, совпадающие с его ребрами:

Построить каждый из следующих векторов:
1)
 ; 2)
; 2)  ; 3)
; 3) 
Решение этой задачи подробно изложено в следующем видео







