Векторно-скалярным (или смешанным) произведением трех векторов  ,
,  и
и 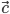 называется число, равное векторному произведению
называется число, равное векторному произведению ![\left[\vec{a}\vec{b} \right]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_115e3d98dc5d51c4cf05a86ba655d378.gif) , умноженному скалярно на вектор
, умноженному скалярно на вектор 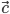 , т. е.
, т. е. ![\left[\vec{a}\vec{b} \right]\vec{c}](https://math-helper.ru/wp-content/plugins/latex/cache/tex_ccef1fd499b02f1d44517790f67ee0ff.gif) .
.
Векторно-скалярное произведение обозначается так:
![\left[\vec{a}\vec{b} \right]\vec{c}=\left(\vec{a}\vec{b} \vec{c}\right)](https://math-helper.ru/wp-content/plugins/latex/cache/tex_fcb5190b4a589a4ba700ef43d0324f7a.gif)
Векторно-скалярное произведение
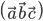 имеет простой геометрический смысл; оно есть число, выражающее объем параллелепипеда, построенного на векторах
имеет простой геометрический смысл; оно есть число, выражающее объем параллелепипеда, построенного на векторах  ,
,  и
и 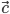 , взятого со знаком плюс, если тройка
, взятого со знаком плюс, если тройка  ,
,  и
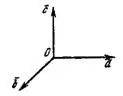
и 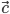 правая, и со знаком минус, если эта тройка левая (рис.1).
правая, и со знаком минус, если эта тройка левая (рис.1).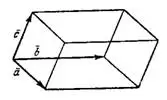
Векторы  ,
,  и
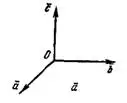
и 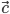 образуют правую тройку, если они расположены, как указано на рисунке 2, и левую тройку, если они расположены, как указано на рисунке 3. Круговая перестановка трех множителей векторно-скалярного произведения не меняет его величины.
образуют правую тройку, если они расположены, как указано на рисунке 2, и левую тройку, если они расположены, как указано на рисунке 3. Круговая перестановка трех множителей векторно-скалярного произведения не меняет его величины.
Перестановка двух соседних множителей меняет знак произведения:

Векторно-скалярное произведение равно нулю, если векторы компланарны.
Следовательно, равенство  есть условие компланарности трех векторов. Если векторы
есть условие компланарности трех векторов. Если векторы  ,
,  и
и 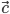 заданы своими проекциями:
заданы своими проекциями:



то векторно-скалярное произведение равно:

Отсюда, объем V параллелепипеда, построенного на векторах
 ,
,  и
и 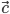 , вычисляется по формуле:
, вычисляется по формуле:
Условие, необходимое и достаточное для компланарности векторов, записывается так:

Объем треугольной пирамиды равен
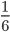 абсолютной величины векторно-скалярного произведения, составленного из трех векторов - ребер, выходящих из одной вершины, т. е:
абсолютной величины векторно-скалярного произведения, составленного из трех векторов - ребер, выходящих из одной вершины, т. е:







