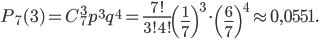Формула Бернулли
Пусть производится n независимых испытаний» в каждом из которых может появиться или не появиться событие  . Вероятность наступления события
. Вероятность наступления события  в каждом испытании постоянна и равна р. Вероятность появления события
в каждом испытании постоянна и равна р. Вероятность появления события  в n испытаниях ровно m раз (безразлично, в какой последовательности) находят по формуле Бернулли
в n испытаниях ровно m раз (безразлично, в какой последовательности) находят по формуле Бернулли
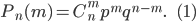
В этой формуле p - вероятность появления события
 в одном испытании; q=1-p - вероятность непоявления события
в одном испытании; q=1-p - вероятность непоявления события  в одном испытании; n - общее число производимых испытаний; m - число испытаний, в которых появится событие
в одном испытании; n - общее число производимых испытаний; m - число испытаний, в которых появится событие  ;
; 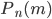 - вероятность того, что событие
- вероятность того, что событие  появится ровно m раз в n испытаниях.
появится ровно m раз в n испытаниях.Задача №1. Вероятность выиграть по одному билету лотереи равна 1/7. Какова вероятность, имея 7 билетов, выиграть
а) по двум билетам;
б) по трем билетам?
Решение. Испытание состоит в проверке одного билета на выигрыш. В каждом испытании может наступить или не наступить событие
 , которое заключается в получении выигрыша на билет. Общее число испытаний n=7. Испытания являются независимыми, так как наступление события
, которое заключается в получении выигрыша на билет. Общее число испытаний n=7. Испытания являются независимыми, так как наступление события  в каждом предыдущем испытании не изменяет вероятности его наступления в последующем. Вероятность появления события
в каждом предыдущем испытании не изменяет вероятности его наступления в последующем. Вероятность появления события  в каждом из семи испытаний постоянна и равна p=1/7; вероятность непоявления события
в каждом из семи испытаний постоянна и равна p=1/7; вероятность непоявления события  в каждом испытании равна q=1-p=1-1/7=6/7.
в каждом испытании равна q=1-p=1-1/7=6/7.а) Обозначим событие:
 - выигрыш по двум билетам из имеющихся семи. Число испытаний, в которых ожидается появление события
- выигрыш по двум билетам из имеющихся семи. Число испытаний, в которых ожидается появление события  , равно m = 2.
, равно m = 2.Искомую вероятность
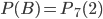 найдем по формуле (1):
найдем по формуле (1):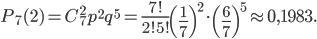
б) Обозначим событие:
 - выигрыш по трем билетам из имеющихся семи.
- выигрыш по трем билетам из имеющихся семи.Число испытаний, в которых ожидается появление события
 , равно m=3.
, равно m=3.Искомую вероятность
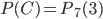 найдем по формуле (1):
найдем по формуле (1):