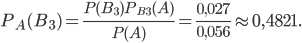Задача №1. В откормочный комплекс поступают телята из трех хозяйств. Из первого хозяйства телят поступает в 2 раза больше, чем из второго, а из второго - в 3 раза больше, чем из третьего. Первое хозяйство поставляет 15% телят, имеющих живой вес более 300 кг. Второе и третье хозяйства поставляют соответственно 25% и 35% телят, живой вес которых превышает 300 кг. Наудачу отобранный теленок при поступлении в откормочный комплекс весит 320 кг. Какова вероятность того, что он поступил из третьего хозяйства?
Решение. Испытание состоит во взвешивании наудачу отобранного теленка из числа поступивших в откормочный комплекс.
Рассмотрим события:
 ,
,  ,
, 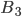 - отобран теленок, поступивший соответственно из 1-го, из 2-го, из 3-го хозяйства;
- отобран теленок, поступивший соответственно из 1-го, из 2-го, из 3-го хозяйства;
 - наудачу отобраний теленок имеет живой вес, превышающий 300 кг.
- наудачу отобраний теленок имеет живой вес, превышающий 300 кг.
Найдем безусловные вероятности гипотез - событий ,
,  и
и 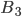 до проведения испытания. Приняв, что из 3-го хозяйства поступает х% телят, получим, что из 2-го и 3-го хозяйств поступает соответственно 3х% и 6х% телят. Общее количество телят, поступающих из этих трех хозяйств, составляет 100%. Таким образом, имеем: 10 х = 100, х = 10. Итак, число телят, поступающих из 1-го, 2-го и 3-го хозяйств составляет соответственно 60%, 30% и 10% от их общего количества. Учитывая это, найдем вероятности гипотез до проведения испытания:
до проведения испытания. Приняв, что из 3-го хозяйства поступает х% телят, получим, что из 2-го и 3-го хозяйств поступает соответственно 3х% и 6х% телят. Общее количество телят, поступающих из этих трех хозяйств, составляет 100%. Таким образом, имеем: 10 х = 100, х = 10. Итак, число телят, поступающих из 1-го, 2-го и 3-го хозяйств составляет соответственно 60%, 30% и 10% от их общего количества. Учитывая это, найдем вероятности гипотез до проведения испытания:
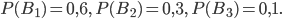
Из 1-го хозяйства поступает 15% теяят, живой вес которых превзашает 300 кг, поэтому
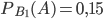 . Аналогично найдем:
. Аналогично найдем: 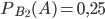 ,
, 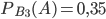 .
.Событие
 может произойти или вместе с событием
может произойти или вместе с событием  , или с событием
, или с событием  , или же с событием
, или же с событием 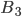 .
.Пусть событие
 произошло. Переоценим вероятность третьей гипотезы - события
произошло. Переоценим вероятность третьей гипотезы - события 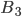 .
.По формуле (1) при n = 3 найдем:
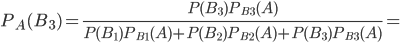
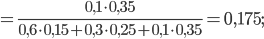
Задача №2. У пользователя имеются три дискеты для компьютера, изготовленные на фирмах K, L и М, по одной дискете от каждой из этих фирм, причем штампы фирм на дискетах отсутствуют. Две из имеющихся трех дискет оказались бракованными. Какова вероятность того, что бракованными являются дискеты фирм L и М, если брак в продукции фирмы К составляет 10%, а в продукции фирм L и М - соответственно 20% и 15%?
Решение. Обозначим событие:  - бракованными являются две дискеты.
- бракованными являются две дискеты.
Событие  может наступить только при условии появления одного из несовместных событий
может наступить только при условии появления одного из несовместных событий 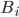 (гипотез), составляющих полную группу. Рассмотрим гипотезы:
(гипотез), составляющих полную группу. Рассмотрим гипотезы:
 - бракованными являются дискеты фирм К и L, а дискета фирмы М - годная;
- бракованными являются дискеты фирм К и L, а дискета фирмы М - годная;
 - бракованными являются дискеты фярм К и М, а дискета фирмы L - годная;
- бракованными являются дискеты фярм К и М, а дискета фирмы L - годная;
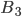 - бракованными являются дискеты фирм L и М, а дискета фирмы К-годная;
- бракованными являются дискеты фирм L и М, а дискета фирмы К-годная;
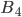 - бракованной является одна дискета;
- бракованной является одна дискета;
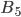 - все три дискеты - бракованные;
- все три дискеты - бракованные;
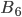 - все три дискеты - годные.
- все три дискеты - годные.
Вероятности гипотез 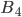 ,
, 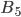 ,
, 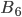 вычислять не нужно, так как при этих гипотезах событие
вычислять не нужно, так как при этих гипотезах событие  невозможно, поэтому условные вероятности
невозможно, поэтому условные вероятности 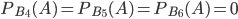 и, следовательно, равны нулю и произведения
и, следовательно, равны нулю и произведения 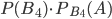 ,
, 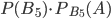 и
и 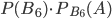 при любых значениях вероятностей гипотез
при любых значениях вероятностей гипотез 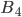 ,
, 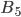 и
и 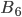 . Рассмотрим события:
. Рассмотрим события:
 - бракованной является дискета фирмы К;
- бракованной является дискета фирмы К;
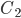 - бракованной является дискета фирмы L;
- бракованной является дискета фирмы L;
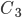 - бракованной является дискета фирмы М, а также противоположные им события:
- бракованной является дискета фирмы М, а также противоположные им события:
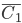 ,
, 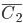 ,
, 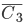 - годной является дискета, соответственно, фирмы К, фирмы L, фирмы М.
- годной является дискета, соответственно, фирмы К, фирмы L, фирмы М.
Исходя из условия, получим: 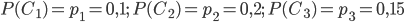 . Найдем:
. Найдем: 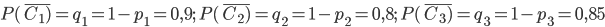
Событие  состоит в совместном наступлении и события
состоит в совместном наступлении и события  и события
и события 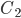 , и события
, и события 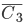 . Это означает, что
. Это означает, что  представляет собой произведение указанных событий:
представляет собой произведение указанных событий: 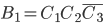 . События
. События  ,
, 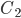 ,
, 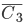 - независимые. Вероятность события
- независимые. Вероятность события  найдем по теореме умножения вероятностей независимых событий:
найдем по теореме умножения вероятностей независимых событий:
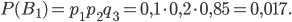
Аналогично получим:
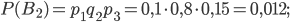
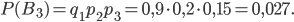
Так как при осуществлении каждой из гипотез  ,
,  и
и 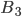 событие
событие  достоверно, то соответствующие условные вероятности равны единице:
достоверно, то соответствующие условные вероятности равны единице:
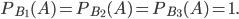
Вероятность того, что бракованными являются две дискеты, найдем по формуле полной вероятности (1) при n = 6:
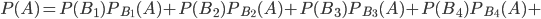
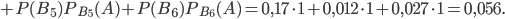
Искомую вероятность того, что бракованными являются дискеты фирм L и М, найдем по формуле Бейеса: