Формула полной вероятности
Вероятность события  , которое может наступить при условии появления одного из n несовместных событий (гипотез)
, которое может наступить при условии появления одного из n несовместных событий (гипотез) 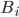 , образующих полную группу, находят по формуле полной вероятности:
, образующих полную группу, находят по формуле полной вероятности:
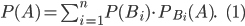
В этой формуле
 - вероятность события
- вероятность события  ;
; 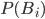 - вероятность события
- вероятность события 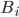 ,
, 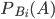 - условная вероятность события
- условная вероятность события  , вычисленная при условии, что событие
, вычисленная при условии, что событие 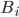 наступило;
наступило;  - сумма произведений вероятностей
- сумма произведений вероятностей 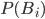 каждого из событий
каждого из событий 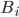 на соответствующую условную вероятность
на соответствующую условную вероятность 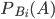 .
.Сумма вероятностей гипотез
 .
.






