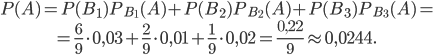Задача №1. Электролампы изготавливают на трех заводах. Первый завод производит 35% общего количества электроламп, второй - 50% и третий - 15%. Продукция первого завода содержит 70% стандартных ламп, второго - 80% и третьего - 90%. В магазин поступает продукция всех трех заводов. Какова вероятность того, что
а) наудачу взятая лампа изготовлена на первом заводе и является стандартной;
б) купленная в магазине лампа является стандартной?
Решение. Рассмотрим события:
 - наудачу взятая лампа изготовлена первым заводом;
- наудачу взятая лампа изготовлена первым заводом;
 - наудачу взятая лампа изготовлена вторым заводом;
- наудачу взятая лампа изготовлена вторым заводом;
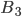 - наудачу взятая лампа изготовлена третьим заводом;
- наудачу взятая лампа изготовлена третьим заводом;
 - наудачу взятая лампа изготовлена на первом заводе и является стандартной;
- наудачу взятая лампа изготовлена на первом заводе и является стандартной;
 - купленная в магазине лампа является стандартной.
- купленная в магазине лампа является стандартной.
Следует учитывать, что первая гипотеза - событие  , заключается в том, что лампа, взятая наудачу из общего количества ламп, изготовленных первым заводом, может быть любого качества, т. е. быть как стандартной, так и нестандартной. Аналогичный смысл имеют две другие гипотезы - события
, заключается в том, что лампа, взятая наудачу из общего количества ламп, изготовленных первым заводом, может быть любого качества, т. е. быть как стандартной, так и нестандартной. Аналогичный смысл имеют две другие гипотезы - события  и
и 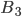 .
.
Вероятности событий  ,
,  и
и 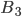 согласно формуле (1) равны:
согласно формуле (1) равны: 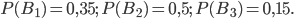 События
События  ,
,  и
и 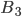 - несовместные и составляют полную группу, сумма вероятностей этих событий равна единице: 0,35 + 0,5 + 0,15 = 1.
- несовместные и составляют полную группу, сумма вероятностей этих событий равна единице: 0,35 + 0,5 + 0,15 = 1.
Из условия следует, что 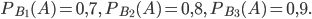
а) Событие  состоит в том, что наудачу взятая лампа, во-первых, изготовлена первым заводом, и, во-вторых, является стандартной. Это означает, что событие
состоит в том, что наудачу взятая лампа, во-первых, изготовлена первым заводом, и, во-вторых, является стандартной. Это означает, что событие  представляет собой произведение двух зависимых событий
представляет собой произведение двух зависимых событий  и
и  :
: 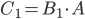 . Вероятность события
. Вероятность события  найдем по теореме умножения вероятностей зависимых событий. Применив формулу (5), получим:
найдем по теореме умножения вероятностей зависимых событий. Применив формулу (5), получим:
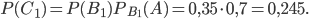
б) Событие
 представляет собой сумму следующих трех несовместных событий:
представляет собой сумму следующих трех несовместных событий: - лампа изготовлена на первом заводе и она стандартная;
- лампа изготовлена на первом заводе и она стандартная;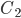 - лампа изготовлена на втором заводе и она стандартная;
- лампа изготовлена на втором заводе и она стандартная;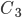 - лампа изготовлена на третьем заводе и она стандартная.
- лампа изготовлена на третьем заводе и она стандартная.Каждое из событий
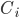 (i = 1,2,3) представляет собой произведение двух зависимых событий
(i = 1,2,3) представляет собой произведение двух зависимых событий 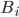 и
и  .
.Таким образом,
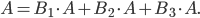 Применив формулу (1), получим
Применив формулу (1), получим
Задача №2. На сборку поступают однотипные изделия из трех цехов. Вероятности изготовления бракованного изделия первым, вторым и третьим цехами соответственно равны 0,03; 0,01 и 0,02. Все поступившие на сборку изделия складывают вместе. Из первого цеха поступает в три раза больше изделий, чем из второго, а из третьего в два раза меньше, чем из второго. Какова вероятность того, что взятое наудачу изделие окажется бракованным?
Решение. Рассмотрим события:
 - взятое изделие поступило из первого цеха;
- взятое изделие поступило из первого цеха; - взятое изделие поступило из второго цеха;
- взятое изделие поступило из второго цеха;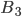 - взятое изделие поступило из третьего цеха;
- взятое изделие поступило из третьего цеха; - взятое изделие является бракованным.
- взятое изделие является бракованным.Первая гипотеза - событие
 , заключается в том, что наудачу взятое изделие, поступившее из первого цеха, может быть любого качества - как бракованным, так и стандартным. Аналогичный смысл имеют две другие гипотезы - события
, заключается в том, что наудачу взятое изделие, поступившее из первого цеха, может быть любого качества - как бракованным, так и стандартным. Аналогичный смысл имеют две другие гипотезы - события  и
и 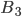 .
.Количество изделий, поступающих на сборку из первого, второго и третьего цехов, определяется соответственно из отношений: 6:2:1. Учитывая эти отношения, найдем вероятности событий
 ,
,  и
и 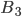 :
: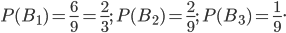
События
 ,
,  и
и 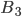 составляют полную группу несовместных событий; сумма вероятностей этих событий равна 1. Событие
составляют полную группу несовместных событий; сумма вероятностей этих событий равна 1. Событие  может наступить или вместе с событием
может наступить или вместе с событием  , или с событием
, или с событием  или с событием
или с событием 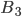 . Условная вероятность события
. Условная вероятность события  , вычисленная при условии, что оно произойдет вместе с событием
, вычисленная при условии, что оно произойдет вместе с событием  равна
равна 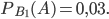 Условные вероятности события
Условные вероятности события  , вычисленные при условиях, что оно произойдет вместе с событиями
, вычисленные при условиях, что оно произойдет вместе с событиями  и
и 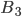 соответственно равны:
соответственно равны: 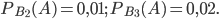
Вероятность события
 найдем по формуле (1) при n=3:
найдем по формуле (1) при n=3: