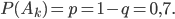Задача №1. Абонент забыл последнюю цифру номера телефона и потому набирает ее наудачу. Какова вероятность того, что ему придется набрать номер не более, чем три раза?
Решение. Обозначим событие:
 - абоненту придется набрать номер не более, чем три раза.
- абоненту придется набрать номер не более, чем три раза.
Это событие состоит в том, что абоненту придется набрать номер или один, или два, или три раза. Рассмотрим следующие события:
 - абонент будет набирать номер один раз;
- абонент будет набирать номер один раз;
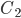 - абонент будет набирать номер два раза;
- абонент будет набирать номер два раза;
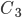 - абонент будет набирать номер три раза;
- абонент будет набирать номер три раза;
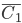 - в первый раз не набрана нужная цифра;
- в первый раз не набрана нужная цифра;
 - во второй раз набрана нужная цифра;
- во второй раз набрана нужная цифра;
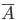 - во второй раз не набрана нужная цифра;
- во второй раз не набрана нужная цифра;
 - в третий раз набрана нужная цифра.
- в третий раз набрана нужная цифра.
Событие  представляет собой сумму несовместных событий
представляет собой сумму несовместных событий  ,
, 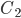 и
и 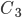 :
:  =
=  +
+ 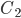 +
+ 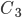 . Вероятность события
. Вероятность события  согласно формуле (1) равна
согласно формуле (1) равна 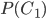 = 1/10.
= 1/10.
Событие 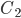 состоит в том, что в первый раз нужная цифра не набрана, а во второй - набрана. Это означает, что
состоит в том, что в первый раз нужная цифра не набрана, а во второй - набрана. Это означает, что 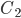 представляет собой произведение событий
представляет собой произведение событий 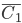 и
и  :
: 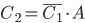 . Вероятность события
. Вероятность события 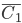 равна
равна 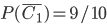 . Событие
. Событие  является зависимым от события
является зависимым от события 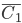 ; условная вероятность
; условная вероятность 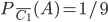 . Вероятность события
. Вероятность события 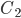 найдем по теореме
найдем по теореме
умножения вероятностей зависимых событий, применив формулу (5), получим: 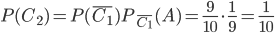 .
.
Событие 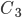 состоит в том, что и в первый, и во второй раз нужная цифра не набрана, а в третий раз - набрана. Это означает, что
состоит в том, что и в первый, и во второй раз нужная цифра не набрана, а в третий раз - набрана. Это означает, что 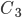 представляет собой произведение зависимых событий
представляет собой произведение зависимых событий 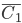 ,
, 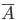 и
и  :
: 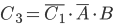 . Условная веpoятнocть
. Условная веpoятнocть 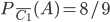 ; условная вероятность
; условная вероятность
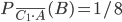 . Вероятность наступления события
. Вероятность наступления события 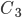 найдем по теореме
найдем по теореме
умножения вероятностей зависимых событий. Применив формулу (7), получим:
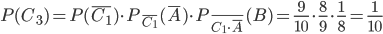 .
.
Искомую вероятность события  найдем по теореме сложения вероятностей несовместных событий. Согласно формуле (9) эта вероятность равна
найдем по теореме сложения вероятностей несовместных событий. Согласно формуле (9) эта вероятность равна
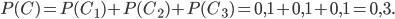
Задача №2. В настольной игре забивают в лунку шарики. Вероятность того, что из четырех шариков ребенок забьет в лунку хотя бы один, равна 0,9919. Какова вероятность забить в лунку каждый из шариков в отдельности, ecли принять, что для всех попыток вероятность забить в лунку шарик одна и та же?
Решение. Рассмотрим события:
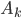 - попадание в лунку k-го шарика (k = 1,2,3,4);
- попадание в лунку k-го шарика (k = 1,2,3,4);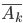 - непопадание в лунку k -го шарика;
- непопадание в лунку k -го шарика; - попадание в лунку хотя бы одного шарика из четырех;
- попадание в лунку хотя бы одного шарика из четырех;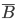 - непопадание в лунку ни одного шарика из четырех.
- непопадание в лунку ни одного шарика из четырех.По условию
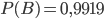 . Требуется найти
. Требуется найти 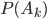 принимая, что
принимая, что 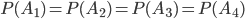 . Обозначим:
. Обозначим: 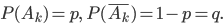
Событие
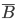 представляет собой произведение четырех независимых событий
представляет собой произведение четырех независимых событий 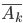 :
: 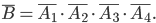
По теореме умножения вероятностей независимых событий получим:
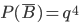 .
.Вероятность события
 равна
равна 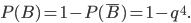 Следовательно,
Следовательно, 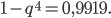 Из последнего уравнения найдем
Из последнего уравнения найдем 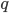 = 0,3. По известному значению
= 0,3. По известному значению 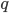 найдем
найдем