Задача №1. Имеется 10 оданаковых по виду урн, в 9-й из которых находятся по 2 черных и 2 белых шара, а в одной - 5 белых и 1 черный. Из наудачу выбранной урны извлечен шар. Извлеченный шар оказался белым. Чему равна вероятность того, что этот шар извлечен из урны, содержащей 5 белых шаров?
Решение. Имеется 2 группы урн с различным составом шаров; 9 из имеющихся урн относятся к первой группе, одна урна - ко второй группе. Испытание состоит в том, что из наудачу выбранной урны извлекается шар. Рассмотрим гипотезы:
 - выбрана урна первой группы;
- выбрана урна первой группы;
 - выбрана урна второй группы и
- выбрана урна второй группы и
событие  - извлечение белого шара.
- извлечение белого шара.
Вероятности гипотез  и
и  равны:
равны: 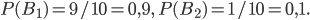 Гипотезы
Гипотезы  и
и  составляют полную группу несовместных событий, сумма вероятностей гипотез равна
составляют полную группу несовместных событий, сумма вероятностей гипотез равна 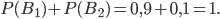
Событие  может произойти только или вместе с событием
может произойти только или вместе с событием  , или с событием
, или с событием  . До проведения испытания условная вероятность события
. До проведения испытания условная вероятность события  , вычисленная при условии, что оно наступило вместе с событием
, вычисленная при условии, что оно наступило вместе с событием  , равна
, равна 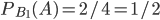 (так как в каждой из урн первой группы среди четырех имеющихся шаров находятся 2 белых шара). До проведения испытания условная вероятность события
(так как в каждой из урн первой группы среди четырех имеющихся шаров находятся 2 белых шара). До проведения испытания условная вероятность события  , вычисленная при условии, что оно наступило вместе с событием
, вычисленная при условии, что оно наступило вместе с событием  , равна
, равна 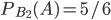 (так как в урне второй группы среди шести имеющихся шаров находятся 5 белых).
(так как в урне второй группы среди шести имеющихся шаров находятся 5 белых).
Пусть событие  произошло: извлеченный из некоторой урны шар - белый. Переоценим вероятность второй гипотезы. По формуле (1) получим
произошло: извлеченный из некоторой урны шар - белый. Переоценим вероятность второй гипотезы. По формуле (1) получим
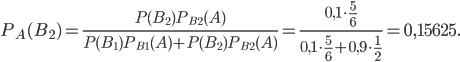
Задача №2. С первого автомата поступает на сборку 80% деталей, а со второго - 20% таких же деталей. На первом автомате брак составляет 1%, а на втором - 5%. Проверенная деталь оказалась бракованной. Что вероятнее: эта деталь изготовлена на первом автомате или же она изготовлена на втором автомате?
Решение. Испытание состоит в проверке качества детали. Рассмотрим события:
 - проверена деталь, изготовленная на первом автомате;
- проверена деталь, изготовленная на первом автомате;
 - проверена деталь, изготовленная на втором автомате;
- проверена деталь, изготовленная на втором автомате;
 - проверенная деталь является бракованной.
- проверенная деталь является бракованной.
Безусловные вероятности гипотез - событий  и
и  до проведения испытания равны:
до проведения испытания равны: 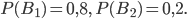 Гипотезы
Гипотезы  и
и  составляют полную группу несовместных событий, сумма вероятностей этих событий равна
составляют полную группу несовместных событий, сумма вероятностей этих событий равна 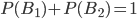 .
.
На первом автомате брак составляет 1%, поэтому 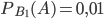 . На втором автомате брак составляет 5%, поэтому
. На втором автомате брак составляет 5%, поэтому 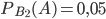 .
.
Событие  может наступить или вместе с событием
может наступить или вместе с событием  , или с событием
, или с событием  .
.
Пусть событие  произошло. Переоценим вероятности гипотез. По формуле Бейеса найдем:
произошло. Переоценим вероятности гипотез. По формуле Бейеса найдем:
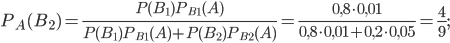
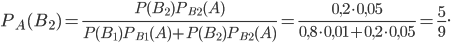
Получено, что . Таким образом, более вероятно, что проверенная деталь, оказавшаяся бракованной, изготовлена на втором автомате.
Задача №3. Изделие проверяется на стандартность одним из двух товароведов. Вероятность того, что изделие попадет к первому товароведу, равна 0,55, а ко второму - 0,45. Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, равна 0,9, а вторым - 0,98. Стандартное изделие при проверке было признано стандартным. Найта вероятность того, что его проверил второй товаровед.
Решение. Испытание состоит в проверке на стандартность одного изделия. Рассмотрим события:
 - изделие проверил первый товаровед;
- изделие проверил первый товаровед;
 - изделие проверил второй товаровед;
- изделие проверил второй товаровед;
 - ставдартное изделие при проверке признано стандартным.
- ставдартное изделие при проверке признано стандартным.
Безусловные вдюятности гипотез - событий  и
и  до проведения испытания равны
до проведения испытания равны 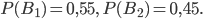 Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, т. е. условная вероятность события
Вероятность того, что стандартное изделие будет признано стандартным первым товароведом, т. е. условная вероятность события  , вычисленная при условии, что оно произошло вместе с событием
, вычисленная при условии, что оно произошло вместе с событием  , равна
, равна 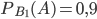 . Вероятность того, что стандартное изделие будет признано стандартным вторым товароведом, т. е. условная вероятность события
. Вероятность того, что стандартное изделие будет признано стандартным вторым товароведом, т. е. условная вероятность события  вычисленная при условии, что оно произошло вместе с событием
вычисленная при условии, что оно произошло вместе с событием  , равна
, равна 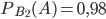 .
.
Известно, что событие  наступило. Переоценим верошность события . По формуле (1) при n = 2 найдем:
наступило. Переоценим верошность события . По формуле (1) при n = 2 найдем:








