Задача №1. У дикорастущей земляники красная окраска ягод доминирует над розовой; этот признак передается по наследству. В некоторой популяции земляники вероятность встретить растение с красными ягодами равна 0,7. Какова вероятность того, что среди отобранных случайным образом 8-ми растений этой популяции красные ягоды будут иметь:
а) б растений;
б) не менее шести растений?
Решение. В каждом испытании может появиться или не появиться событие  , которое состоит в том, что у растения земляники будут красные ягоды. Общее число испытаний n = 8; испытания являются независимыми. Вероятность появления события
, которое состоит в том, что у растения земляники будут красные ягоды. Общее число испытаний n = 8; испытания являются независимыми. Вероятность появления события  в каждом из восьми испытаний постоянна и равна р=0,7; вероятность непоявления события
в каждом из восьми испытаний постоянна и равна р=0,7; вероятность непоявления события  в каждом испытании равна q = 1 - р = 0,3.
в каждом испытании равна q = 1 - р = 0,3.
а) Обозначим событие:
 - ровно б растений из восьми отобранных будут иметь красные ягоды. Число испытаний, в которых ожидается появление события
- ровно б растений из восьми отобранных будут иметь красные ягоды. Число испытаний, в которых ожидается появление события  , равно
, равно 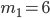 .
.
Искомую вероятность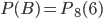 найдем по формуле (1) при значении
найдем по формуле (1) при значении 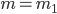 :
:
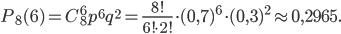
б) Обозначим событие:
 - не менее шести растений из восьми отобранных будут иметь красные ягоды.
- не менее шести растений из восьми отобранных будут иметь красные ягоды.Рассмотрим события, составляющие событие
 :
: ,
, 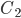 ,
, 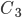 - красные ягоды будут иметь, соответственно, б растений, 7 растений, 8 растений из 8 отобранных.
- красные ягоды будут иметь, соответственно, б растений, 7 растений, 8 растений из 8 отобранных.  ,
, 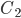 ,
, 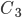 - несовместные события, причем событие
- несовместные события, причем событие  равно событию
равно событию  , рассмотренному в пункте а) задачи.
, рассмотренному в пункте а) задачи.Событие
 состоит в том, что красные ягоды будут иметь или б, или 7, или 8 растений. Это означает, что событие
состоит в том, что красные ягоды будут иметь или б, или 7, или 8 растений. Это означает, что событие  представляет собой сумму событий
представляет собой сумму событий  ,
, 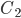 и
и 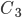 :
: 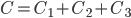 . Вероятность события
. Вероятность события  найдем по теореме сложения вероятностей несовместных событий:
найдем по теореме сложения вероятностей несовместных событий: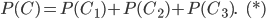
Вероятность
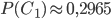 . Вероятности
. Вероятности 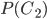 и
и 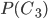 найдем по формуле Бернулли при значениях m, соответственно равных
найдем по формуле Бернулли при значениях m, соответственно равных 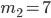 и
и 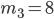 :
: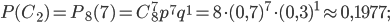
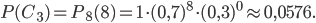
Подставив значения 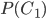 ,
, 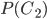 и
и 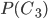 в равенство (*), получим
в равенство (*), получим
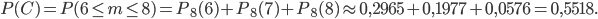
В рассмотренном случае вероятность 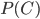 равна вероятности того, что событие
равна вероятности того, что событие  появится в 8-ми испытаниях от
появится в 8-ми испытаниях от 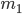 до
до 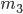 раз. Итак, при небольших значениях
раз. Итак, при небольших значениях 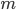 и
и  вероятность того, что
вероятность того, что 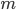 примет определенное значение из заданного интервала, находят с применением формулы Бернулли и теоремы сложения вероятностей несовместных событий.
примет определенное значение из заданного интервала, находят с применением формулы Бернулли и теоремы сложения вероятностей несовместных событий.
Задача №2. Исследование инкубации яиц яичного кросса Беларусь-9 показало, что цыплята выводятся в среднем из 70% заложенных в инкубатор яиц. Из общего количества заложенных в инкубатор яиц случайным образом отобраны и помечены шесть. Найти вероятности того, что из помеченных яиц выведутся:
а) менее трех цыплят;
б) более трех цыплят;
в) не менее трех цыплят;
г) не более трех цыплят.
д) Есть ли среди событий, вероятности которых требуется найти в пунктах: а) - г), такие, которые составляют полную группу? (если есть, то какие?).
Решение. Общее число независимых испытаний n = 6. Событие  , которое может произойти или не произойти в каждом испытании, состоит в том, что из заложенного в инкубатор яйца выведется цыпленок. Вероятность наступления события
, которое может произойти или не произойти в каждом испытании, состоит в том, что из заложенного в инкубатор яйца выведется цыпленок. Вероятность наступления события  в каждом испытании постоянна и равна р = 0,7; вероятность q = 0,3.
в каждом испытании постоянна и равна р = 0,7; вероятность q = 0,3.
Рассмотрим события:
 - из б-ти яиц выведутся менее трех цыплят;
- из б-ти яиц выведутся менее трех цыплят;
 - из 6-ти яиц выведутся более трех цыплят;
- из 6-ти яиц выведутся более трех цыплят;
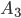 - из 6-ти яиц выведутся не менее трех цыплят;
- из 6-ти яиц выведутся не менее трех цыплят;
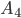 - из 6-ти яиц выведутся не более трех цыплят.
- из 6-ти яиц выведутся не более трех цыплят.
По формуле Бернулли найдем:
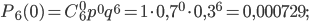
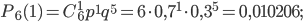
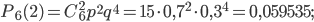
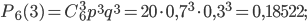
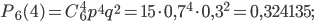
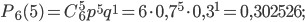
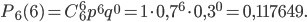
Вероятности событий  ,
,  ,
, 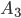 и
и 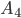 найдем, применив формулу Бернулли и теорему сложения вероятностей несовместных событий:
найдем, применив формулу Бернулли и теорему сложения вероятностей несовместных событий:
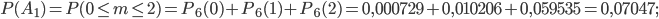
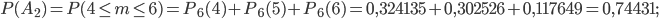
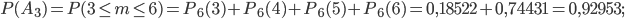
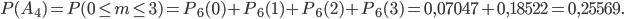
События  и
и 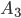 составляют полную группу несовместных событий, так как событие
составляют полную группу несовместных событий, так как событие 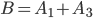 достоверно.
достоверно.
Вероятность этого события 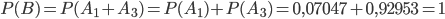 .
.
События  и
и 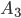 - взаимно противоположные; можно обозначить:
- взаимно противоположные; можно обозначить: 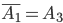 .
.
Так же можно показать, что полную группу несовместных событий составляют события  и
и 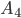 . События
. События  и
и 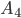 - взаимно противоположные; можно обозначить:
- взаимно противоположные; можно обозначить: 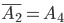 .
.







