Задача №1.В Московской области при выращивании озимой ржи сорта Чулпан с применением почвозащитных технологий обработки почвы и средств химизации вероятность гибели более 92% всех сорняков равна 0,8. На опытном поле, разбитом на делянки, случайным образом выбрано 5 делянок. Найти вероятность того, что не менее, чем на двух из них погибнет более 92% сорняков.
Решение. Испытание состоит в проверке факта гибели более 92% сорняков на одной делянке. Общее число испытаний n = 5. Все испытания являются независимыми. Событие  , которое может произойти или не произойти в каждом испытании - гибель более 92% сорняков. Вероятность р = 0,8, вероятность q = 0,2. Рассмотрим событие:
, которое может произойти или не произойти в каждом испытании - гибель более 92% сорняков. Вероятность р = 0,8, вероятность q = 0,2. Рассмотрим событие:
 - более 92% сорняков погибнет не менее, чем на двух делянках из пяти.
- более 92% сорняков погибнет не менее, чем на двух делянках из пяти.
Вероятность события в представляет собой вероятность того, что число m появлений события  в пяти испытаниях будет больше или равно двум и меньше или равно пяти. Искомая вероятность равна
в пяти испытаниях будет больше или равно двум и меньше или равно пяти. Искомая вероятность равна
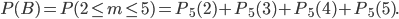
Каждое из четырех слагаемых в последнем равенстве найдем по формуле Бернулли.
Решение будет более коротким, если рассмотреть событие 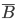 , противоположное событию
, противоположное событию  . Событие
. Событие 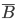 состоит в том, что более 92% сорняков погибнет менее, чем на двух делянках, т. е. или ни на одной, или на одной делянке. Воспользовавшись формулой (4) для определения вероятности противоположного события и теоремой сложения вероятностей несовместных событий, получим
состоит в том, что более 92% сорняков погибнет менее, чем на двух делянках, т. е. или ни на одной, или на одной делянке. Воспользовавшись формулой (4) для определения вероятности противоположного события и теоремой сложения вероятностей несовместных событий, получим
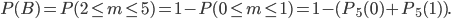
Вероятности 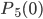 и
и 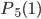 найдем по формуле Бернулли. Таким образом,
найдем по формуле Бернулли. Таким образом,
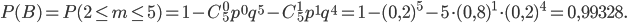
Задача №2. Вероятность того, что из четырех кустов садовой земляники сорта Талисман, отобранных с некоторого участка случайным образом, хотя бы один куст поражен вилтом, равна 0,3439. Какова вероятность поражения вилтом одного куста земляники, если для всех кустов эта вероятность одинакова?
Решение. Испытание состоит в проверке одного куста земляники. Общее число испытаний n = 4. Испытания являются независимыми. Событие  , которое может появится или не появится в каждом испытании, состоит в том, что проверенный куст поражен вилтом. Рассмотрим события:
, которое может появится или не появится в каждом испытании, состоит в том, что проверенный куст поражен вилтом. Рассмотрим события:
 - вилтом поражен хотя бы один куст из четырех кустов земляники;
- вилтом поражен хотя бы один куст из четырех кустов земляники;
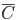 - ни один из четырех кустов не поражен вилтом.
- ни один из четырех кустов не поражен вилтом.
Событие 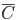 противоположно событию
противоположно событию  . Используя формулу (4) для определения вероятности противоположного события и формулу (1), по которой найдем
. Используя формулу (4) для определения вероятности противоположного события и формулу (1), по которой найдем 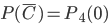 , получим:
, получим:
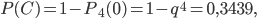
где
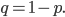
Решив уравнение
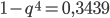 , найдем q = 0,9 ; отсюда получим p = 0,1.
, найдем q = 0,9 ; отсюда получим p = 0,1.Задача №3. Две электрические лампочки включены в цепь параллельно. Вероятность того, что при некотором повышении напряжения в цепи выше номинального перегорит только одна лампочка, равна 0,18. Найти вероятности перегореть для каждой из этих лампочек, если известно, что эти вероятности превосходят 0,7 и равны между собой.
Решение. Испытание состоит в проверке работы электрической лампочки. Общее число испытаний n =2. Испытания являются независимыми. Событие  , которое может произойти или не произойти в каждом испытании, состоит в том, что при повышении напряжения в цепи лампочка не перегорит. Известна вероятность того, что не перегорит только одна лампочка (без указания, какая именно). Так как вероятности наступления события
, которое может произойти или не произойти в каждом испытании, состоит в том, что при повышении напряжения в цепи лампочка не перегорит. Известна вероятность того, что не перегорит только одна лампочка (без указания, какая именно). Так как вероятности наступления события  в каждом испытании равны между собой, то известна вероятность
в каждом испытании равны между собой, то известна вероятность 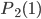 , определяемая по формуле Бернулли. По условию
, определяемая по формуле Бернулли. По условию 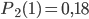 . Требуется найти вероятность р наступления события
. Требуется найти вероятность р наступления события  в каждом испытании.
в каждом испытании.
По формуле Бернулли получим
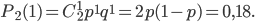
Отсюда следует, что неизвестная вероятность р может быть найдена как корень квадратного уравнения
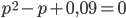 . Это уравнение имеет два корня:
. Это уравнение имеет два корня: 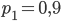 и
и 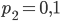 . По условию , поэтому задаче удовлетворяет лишь первый корень. Таким образом, вероятность того, что каждая из лампочек не перегорит, равна
. По условию , поэтому задаче удовлетворяет лишь первый корень. Таким образом, вероятность того, что каждая из лампочек не перегорит, равна 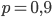 .
.






