Геометрические места точек
Линия может быть определена как некоторое геометрическое место точек, т. е. может быть дано геометрическое свойство, присущее только точкам этой линии. В таком случае возникает вопрос о нахождении уравнения линии.
Задача нахождения уравнения линии сводится к тому, чтобы выразить аналитически тот факт, что все точки линии обладают определенным свойством. Но нет необходимости рассматривать все точки линии. Мы можем представить себе, что эта линия описана подвижной точкой М (х,у).
Поэтому для составления уравнения берут произвольную точку, принадлежащую данному геометрическому месту, и связывают ее координаты х и у с данными величинами.
Получив искомое уравнение, доказывают, что это и есть уравнение данного геометрического места, что координаты точек, не принадлежащих данному геометрическому месту, не удовлетворяют найденному уравнению.
Решение задач на геометрические места значительно упрощается, если удачно подобрать соответствующую систему осей координат.
Примерами на составление уравнений геометрических мест могут служить выводы канонических уравнений окружности, эллипса, гиперболы и параболы.
Задача. Составить уравнение геометрического места точек, одинаково удаленных от начала координат и от точки А (—5;3).
Решение. Пусть точка М (х, у) лежит на искомом геометрическом месте (рис.1).
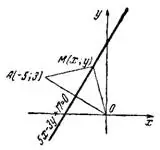
Тогда, согласно условию, МА=МО, т. е. расстояния точки М(х,у) до точки А (-5;3) и начала координат О равны между собой:
Тогда в силу равенства МА=МО, имеем
или х²+10х+25+у²-6у+9=х²+у², и окончательно 5x-3y+17=0.
Итак, искомое геометрическое место точек есть прямая, перпендикулярная АО и делящая этот отрезок пополам. Покажем теперь, что координаты точек, не принадлежащих прямой, перпендикулярной к АО и делящей отрезок АО пополам, не удовлетворяют найденному уравнению 5x-3y+17=0.
Пусть точка М(х, у) не принадлежит найденному геометрическому месту точек. Тогда либо МА>МO либо МА<МО.
Если МА>МO, тогда 
или х²+10x+25+y²-6y+9>x²+y², и окончательно 5x+3y+17>0.
Следовательно, точка М (х,у) не удовлетворяет уравнению геометрического места 5х-Зу+17=0. Для случая МА<МО доказательство аналогично.
