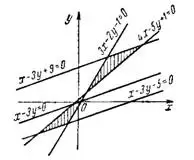
Задача № 1. Составить уравнения прямых, параллельных прямой x-3y=0 и отсекающих от двух пересекающихся прямых Зх-2у-1=0, 4х-5y+1=0 треугольник, площадь которого равна 7/2.
Решение. Уравнения искомых прямых будут х-3у+с=0.
Коэффициент с определим, использовав площадь треугольника.
Найдем координаты вершин треугольника, имеющего площадь 7/2, для чего решим следующие системы уравнений:
![]()
Решаем первую, вторую и третью системы уравнений.
Получим координаты точек: А (1; 1),
![]()
Подставив в эту формулу соответствующие значения
![]()
Подставив в эту формулу соответствующие значения х₁, х₂, х₃ и у₁, у₂, у₃ получим выражение площади
![]()
По условию площадь этого треугольника равна 7/2, т. е.
![]()
или
![]()
Так как квадрат действительного числа не может быть отрицательным, то рассмотрим только уравнение
(с —2)² = 49. Решим его: с-2=±7, с₁=2+7=9, c₂=2-7=-5.
Таким образом, уравнениями искомых прямых будут уравнения: х-3y+9=0 и х-Зу-5=0. (рис.1).
Ответ: х-3y+9=0, х-Зу-5=0.
Решение этой задачи подробно изложено в следующем видео
Задача № 2. Найти полярное уравнение прямой, если:
1) Угол наклона прямой к полярной оси равен 1/6π, а длина перпендикуляра, опущенного из полюса на эту прямую, равна 3.
2) Отрезок, отсекаемый прямой на полярной оси, равен 2, а полярный угол нормали этой прямой равен -2/3π.
3) Угол наклона прямой к полярной оси равен 1/6π и отрезок, который отсекает прямая на полярной оси, равен 6.
Решение этой задачи подробно изложено в следующем видео







