Задача № 1. Составить уравнение прямой, если известно, что ее расстояние от начала координат равно 13, а угол, образованный перпендикуляром, опущенным с начала координат на прямую, и осью Ох, равен 225°.
Решение этой задачи подробно изложено в следующем видео
Задача № 2. Провести прямую через точку Р (3;-4), являющуюся основанием перпендикуляра, опущенного из начала координат на прямую.
Решение этой задачи подробно изложено в следующем видео
Задача № 3. Найти геометрическое место точек, отклонение которых от прямой 6х-8y+5=0, равно 5.
Задача № 4. Найти геометрическое место точек, расстояние которых от прямой 5х-12у-13=0 равно 3.
Решения этих двух задач подробно объясняются в следующем видео:
Задача № 5. Две стороны квадрата лежат на прямых 4х-Зу+15=0 и 8х-6y+25=0. Вычислить его площадь.
Задача № 6. Доказать, что через точку Р(2;7) можно провести две прямые так, чтобы их расстояния от точки Q(1;2) были равны 5. Составить уравнения этих прямых.
Решения этих двух задач подробно объясняются в следующем видео:
Задача № 7. Составить уравнения прямых, перпендикулярных к прямой 2х+6y-3=0 и отстоящих от точки (5;4) на расстоянии V10 ед.
Решение этой задачи подробно изложено в следующем видео
Задача № 8. На прямой х+у-8=0 найти точки, равноудаленные от точки (2;8) и от прямой х-Зy+2=0.
Решение этой задачи подробно изложено в следующем видео
Задача № 9. Найти биссектрисы углов между прямыми Зх+4у-1=0 и 4х-Зy+5=0.
Решение этой задачи подробно изложено в следующем видео
Задача № 10. Даны вершины треугольника А (2; —2), В (3; -5) и С (5; 1). Составить уравнение перпендикуляра, опущенного из вершины С на биссектрису внутреннего угла при вершине В.
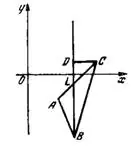
Решение. Чтобы составить уравнение перпендикуляра CD (рис.1), опущенного на биссектрису BD, необходимо знать угловой коэффициент BD. Для этого достаточно найти координаты точки L, которая согласно свойству биссектрисы внутреннего угла треугольника делит сторону АС в отношении
![]()
Для определения λ необходимо найти длины сторон АВ и ВС, которые находим по формуле расстояния между двумя точками.
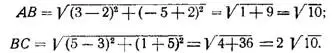
Таким образом, ![]()
Координаты точки L найдем по формулам деления отрезка в заданном отношении:
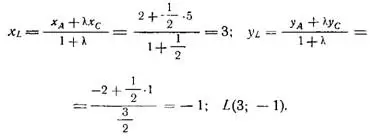
Угловой коэффициент BD найдем по формуле
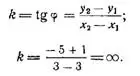
Следовательно, биссектриса BD перпендикулярна к оси Ох.
В таком случае прямая CD будет параллельна оси Ох, ее уравнение у = b, где b — ордината точки, через которую проходит прямая. b=1.
Таким образом, уравнением перпендикуляра CD будет уравнение у = 1, или у —1=0.
Ответ: у —1=0.
Решение этой задачи подробно изложено в следующем видео







