Иррациональные (и трансцендентные) функции интегрируются в элементарных функциях только в некоторых определенных случаях. Наиболее употребительны следующие виды интегралов от иррациональных функций, которые выражаются через элементарные функции:
I. Интеграл  , где
, где 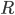 — рациональная функция,
— рациональная функция,
 — рациональные числа, сводится к интегралу от рациональной функции, и, следовательно, выражается в элементарных функциях с помощью подстановки
— рациональные числа, сводится к интегралу от рациональной функции, и, следовательно, выражается в элементарных функциях с помощью подстановки  , где
, где 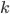 — общий знаменатель всех дробных показателей у
— общий знаменатель всех дробных показателей у  .
.
Интегралы более общего вида ![\displaystyle \int R\left [ x,(ax+b)^{\alpha },(ax+b)^{\beta },... \right ]dx](https://math-helper.ru/wp-content/plugins/latex/cache/tex_37c17cb8745789ed2488341bff01f474.gif) или
или ![\displaystyle \int R\left [ x,\left ( \frac{ax+b}{cx+d} \right )^{\alpha },\left ( \frac{ax+b}{cx+d} \right )^{\beta },... \right ]dx](https://math-helper.ru/wp-content/plugins/latex/cache/tex_9eed82367a54064f62792b5eba8437d8.gif) находятся (приводятся к рациональному виду) с помощью аналогичных подстановок:
находятся (приводятся к рациональному виду) с помощью аналогичных подстановок:  или
или  .
.
II. К интегралам от функций, рационально зависящих от тригонометрических функций, сводятся интегралы:
 — подстановкой
— подстановкой  ;
;
 — подстановкой
— подстановкой  ;
;
 — подстановкой
— подстановкой  .
.
III. Интеграл от дифференциального бинома  сводится к интегралу от рациональной функции в трех случаях:
сводится к интегралу от рациональной функции в трех случаях:
1) когда  — целое число, — разложением на слагаемые по формуле бинома Ньютона,
— целое число, — разложением на слагаемые по формуле бинома Ньютона,
2) когда  - целое число, — подстановкой
- целое число, — подстановкой  ,
,
3) когда  — целое число, — подстановкой
— целое число, — подстановкой  , где
, где 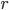 — знаменатель дроби
— знаменатель дроби  .
.
IV. Интеграл  , где
, где  — многочлен
— многочлен  -й степени,
-й степени,  , можно найти по формуле
, можно найти по формуле

где
 — постоянные, определяемые путем дифференцирования этого равенства, умножения его на
— постоянные, определяемые путем дифференцирования этого равенства, умножения его на  и сравнения коэффициентов при одинаковых степенях
и сравнения коэффициентов при одинаковых степенях  . Подобным путем можно найти и интеграл
. Подобным путем можно найти и интеграл
V. Интеграл
 можно найти подстановкой
можно найти подстановкой  .
.






