Интегрирование по частям. Практикум по математическому анализу. Урок 72

Из формулы дифференциала произведения $d(uv)=udv+vdu$ интегрированием обеих частей равенства получается формула интегрирования по частям:

$$\displaystyle \int udv=uv-\int vdu.\; \; \; \; (*)$$

По этой формуле отыскание интеграла $\displaystyle \int udv$ сводится к отысканию другого интеграла $\displaystyle \int vdu$. Применение ее целесообразно в тех случаях, когда последний интеграл будет проще исходного или когда он будет ему подобен.
Для применения формулы интегрирования по частям к некоторому интегралу $\displaystyle \int f(x)dx$ следует подынтегральное выражение $f(x)dx$ представить в виде произведения двух множителей: $u$ и $dv$; за $dv$ всегда выбирается такое выражение, содержащее $dx$, из которого посредством интегрирования можно найти $v$; за $u$ в большинстве случаев принимается функция, которая при дифференцировании упрощается (например: $\displaystyle \textrm{arcsin}\, x,\: \textrm{arctg}\, 3x,\: \ln x,\: x^{3}$).
Пример 1. Найти интегралы:
1) $\displaystyle \int x\cos xdx;$
2) $\displaystyle \int \frac{\ln x}{x^{3}}dx;$
3) $\displaystyle \int x \textrm{arctg}\, xdx;$
4) $\displaystyle \int \textrm{arcsin}\, xdx;$
5) $\displaystyle \int x^{2}e^{3x}dx;$
6) $\displaystyle \int e^{-x}\cos \frac{x}{2}dx.$
Решение.
1) Положив $\displaystyle u=x,\: dv=\cos xdx$, найдем: $\displaystyle du=dx,\: v=\int \cos xdx=\sin x$. Подставляя в формулу (*), получим

$$\displaystyle \int x\cos xdx=x\sin x-\int \sin xdx=x\sin x+\cos x+C.$$

2) Пусть $\displaystyle u=\ln x,\: dv=\frac{dx}{x^{3}}$, тогда $\displaystyle du=\frac{dx}{x},\: v=\int \frac{dx}{x^{3}}=\int x^{-3}dx=-\frac{1}{2x^{2}}$. Подставляя в формулу (*), найдем

$$\displaystyle \int \frac{\ln x}{x^{3}}dx=-\frac{\ln x}{2x^{2}}-\int -\frac{1}{2x^{2}}\cdot \frac{dx}{x}=-\frac{\ln x}{2x^{2}}-\frac{1}{4x^{2}}+C=C-\frac{1+2\ln x}{4x^{2}}.$$

3) Пусть $\displaystyle u=\textrm{arctg}\, x,\: dv=xdx$, тогда $\displaystyle du=\frac{dx}{1+x^{2}},\: v=\int xdx=\frac{x^{2}}{2}$.
По формуле (*), получим

$$\displaystyle I=\int x \textrm{arctg}\, xdx=\frac{x^{2}}{2}\textrm{arctg}\, x-\frac{1}{2}\int \frac{x^{2}}{1+x^{2}}dx.\; \; (1)$$

Последний интеграл находим отдельно:
$\displaystyle \int \frac{x^{2}}{1+x^{2}}dx=\int \frac{1+x^{2}-1}{1+x^{2}}dx=\int \left ( 1-\frac{1}{1+x^{2}} \right )dx=x-\textrm{arctg}\, x.$
Подставляя этот результат в равенство (1), имеем
$\displaystyle I=\frac{x^{2}}{2}\textrm{arctg}\, x-\frac{x}{2}+\frac{1}{2}\textrm{arctg}\, x+C=C-\frac{x}{2}+\frac{x^{2}+1}{2}\textrm{arctg}\, x.$
4) Полагая $\displaystyle u=\textrm{arcsin}\, x,\: dv=dx$, найдем: $\displaystyle du=\frac{dx}{\sqrt{1-x^{2}}},\: v=\int dx=x$. По формуле (*) получим

$$\displaystyle J=\int \textrm{arcsin}\, xdx=x\textrm{arcsin}\, x-\int \frac{xdx}{\sqrt{1-x^{2}}}.\; \; \; \; (2)$$

Последний интеграл найдем, преобразуя его к формуле 1:

$$\displaystyle \int \frac{xdx}{\sqrt{1-x^{2}}}=-\frac{1}{2}\int (1-x^{2})^{-\frac{1}{2}}(-2xdx)=-\frac{1}{2}\int (1-x^{2})^{-\frac{1}{2}}d(1-x^{2})=-(1-x^{2})^{\frac{1}{2}}.$$

Подставляя в равенство (2), имеем

$$\displaystyle J=x\textrm{arcsin}\, x+\sqrt{1-x^{2}}+C.$$

5) Положим $\displaystyle u=x^{2},\: dv=e^{3x}dx$, тогда $\displaystyle du=2xdx,\: v=\int e^{3x}dx=\frac{1}{3}\int e^{3x}d(3x)=\frac{1}{3}e^{3x}$. По формуле (*) найдем

$$\displaystyle I=\int x^{2}e^{3x}dx=\frac{x^{2}}{3} e^{3x}-\frac{2}{3}\int xe^{3x}dx.\; \; \; \; \; (3)$$

К последнему интегралу вновь применяем формулу интегрирования по частям. Положим $\displaystyle u=x,\: dv=e^{3x}dx$, тогда $\displaystyle du=dx,\: v=\int e^{3x}dx=\frac{1}{3}e^{3x}$. По формуле (*) получим

$$\displaystyle \int xe^{3x}dx=\frac{x}{3}e^{3x}-\frac{1}{3}\int e^{3x}dx=\frac{x}{3}e^{3x}-\frac{1}{9}e^{3x}.$$

Подставляя в (3), имеем

$$\displaystyle I=\frac{x^{2}}{3}e^{3x}-\frac{2}{3}\left ( \frac{x}{3}e^{3x}-\frac{1}{9}e^{3x} \right )+C=\frac{e^{3x}}{27}(9x^{2}-6x+2)+C.$$

Здесь понадобилось применить формулу (*) дважды. Очевидно, если бы под интегралом вместо 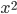$x^{2}$ было $x^{3}$, то пришлось бы эту формулу применить три раза. Вообще, для нахождения интеграла $\displaystyle \int x^{n}e^{x}dx$, а также и интегралов $\displaystyle \int x^{n}\sin xdx,\: \int x^{n}\cos xdx$ ($n$ — целое положительное число) требуется применить интегрирование по частям $n$ раз.
6) Пусть $\displaystyle u=e^{-x},\: dv=\cos \frac{x}{2}dx$, тогда $\displaystyle du=-e^{-x}dx,\: v=\int \cos \frac{x}{2}dx=2\int \cos \frac{x}{2}d\left ( \frac{x}{2} \right )=2\sin \frac{x}{2}$. По формуле (*) имеем

$$\displaystyle I=\int e^{-x}\cos \frac{x}{2}dx=2e^{-x}\sin \frac{x}{2}+2\int e^{-x}\sin \frac{x}{2}dx.\; \; \; (4)$$

К полученному интегралу I снова применяем интегрирование по частям. Полагая $\displaystyle u=e^{-x},\: dv=\sin \frac{x}{2}dx$, получим $\displaystyle du=-e^{-x},\: v=\int \sin \frac{x}{2}dx=2\int \sin \frac{x}{2}d\left ( \frac{x}{2} \right )=-2\cos \frac{x}{2}$,

$$\displaystyle I_{1}=\int e^{-x} \sin \frac{x}{2}dx=-2e^{-x}\cos \frac{x}{2}-2\int e^{-x}\cos \frac{x}{2}dx=-2e^{-x}\cos \frac{x}{2}-2I.$$

Подставляя этот результат в (4), получим уравнение с неизвестным интегралом I:

$$\displaystyle I=2 e^{-x} \sin \frac{x}{2}+2\left ( -2e^{-x}\cos \frac{x}{2}-2I \right ),$$

из которого находим

$$\displaystyle 5I=2 e^{-x} \sin \frac{x}{2}-4e^{-x}\cos \frac{x}{2},\: I=\frac{2}{5}e^{-x}\left ( \sin \frac{x}{2}-2\cos \frac{x}{2} \right )+C.$$

Если при отыскании $I_{1}$ выбрать $u$ и $dv$ иначе: $\displaystyle u=\sin \frac{x}{2},\: dv=e^{-x}dx$, то получим $\displaystyle du=\frac{1}{2}\cos \frac{x}{2}dx,\: v=-e^{-x},$
$\displaystyle I_{1}=-e^{-x}\sin \frac{x}{2}+\frac{1}{2}\int e^{-x}\cos \frac{x}{2}dx=-e^{-x}\sin \frac{x}{2}+\frac{1}{2}I.$
Подставляя $I_{1}$ в равенство (4), получим бесполезное тождество

$$\displaystyle I=2e^{-x}\sin \frac{x}{2}+2\left ( -e^{-x}\sin \frac{x}{2}+\frac{1}{2}I \right );\: 0=0.$$

Это решение показывает, что повторное интегрирование по частям может привести к исходному интегралу I. В таком случае получается или уравнение, из которого легко найти I, или, при неудачном выборе $u$ и $dv$ в повторном интегрировании, бесполезное тождество.