Часто встречающиеся интегралы от выражений, содержащих тригонометрические функции следующих видов:
I.  , II.
, II.  , III.
, III.  , где
, где 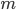 и
и  — целые положительные числа.
— целые положительные числа.
IV.  .
.
можно свести к формулам интегрирования, а следовательно, и найти, руководствуясь следующими правилами:
1. Интегралы от четной степени синуса или косинуса можно найти путем понижения степени (вдвое) по формулам:

2. Интегралы от нечетной степени синуса или косинуса можно найти путем отделения от нее одного множителя и замены кофункции новой переменной.
3. Интегралы вида II можно найти по правилу 1, если тип оба четные, или по правилу 2, если 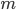 или
или  (или и
(или и 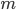 и
и  ) нечетно.
) нечетно.
4. Интегралы вида III можно найти путем замены  , или соответственно,
, или соответственно,  новой переменной.
новой переменной.
5. Интегралы вида IV можно найти путем разложения на слагаемые по формулам:
![\displaystyle \sin ax\cos bx=\frac{1}{2}\left [ \sin (a+b)x+\sin (a-b)x \right ],](https://math-helper.ru/wp-content/plugins/latex/cache/tex_9d5ece4601946ef33a0ca563490629d5.gif)
![\displaystyle \sin ax\sin bx=\frac{1}{2}\left [ \cos (a-b)x-\cos (a+b)x \right ],](https://math-helper.ru/wp-content/plugins/latex/cache/tex_68ddb98ad44998773854f3cc29f858f3.gif)
![\displaystyle \cos ax\cos bx=\frac{1}{2}\left [ \cos (a+b)x+\cos (a-b)x \right ].](https://math-helper.ru/wp-content/plugins/latex/cache/tex_3057d9c2346c33f4bd45305917f38e80.gif)
Пример 1. Найти интегралы:
1)  ;
;
2)  ;
;
3)  ;
;
4)  ;
;
5)  ;
;
6)  .
.
Решение. 1) Согласно правилу 1 имеем

2) Применяя правило 1, получим
![\displaystyle \int \cos ^{4}xdx=\int (\cos ^{2}x)^{2}dx=\frac{1}{4}\int (1+\cos 2x)^{2}dx=\frac{1}{4}\left [ \int dx+\int \cos 2xd(2x)+\int \cos ^{2}2xdx \right ].](https://math-helper.ru/wp-content/plugins/latex/cache/tex_ba13cf424960e76dd5ba6eb00a0d6df1.gif)
Первые два интеграла представляют формулы, последний интеграл находим отдельно, по правилу 1:

Подставляя в предыдущее равенство, получим

3) По правилу 2 отделяем от нечетной степени один множитель  и заменяем кофункцию новой переменной, т. е. полагаем
и заменяем кофункцию новой переменной, т. е. полагаем  . Тогда получим
. Тогда получим  .
.


4) Применяя правило 3 (1), получим


Первый интеграл находим по правилу 1:

Второй интеграл находим по правилу 3 (2), полагая  . Тогда
. Тогда  ,
,

Подставляя эти результаты, имеем

5) Согласно правилу 3(2) отделяем от нечетной степени один множитель  и заменяем кофункцию новой переменной, т. е. полагаем
и заменяем кофункцию новой переменной, т. е. полагаем  . Тогда имеем
. Тогда имеем  ,
,


6) Применяем правило 3(2): отделяем от одной из нечетных степеней (низшей) один множитель  и заменяем
и заменяем  через
через  ; тогда найдем:
; тогда найдем:  и
и


Пример 2. Найти интегралы: 1)  ; 2)
; 2)  .
.
Решение: 1) Применяя правило 4, полагаем  , тогда
, тогда  ,
,


2) Применяем правило 5; разлагаем подынтегральную функцию на слагаемые, пользуясь тригонометрической формулой, затем интегрируем:
![\displaystyle \int \sin 3x\cos 5xdx=\frac{1}{2}\int \left [ \sin 8x+\sin (-2x) \right ]dx=\frac{1}{16}\int \sin 8xd(8x)-\frac{1}{4}\int \sin 2xd(2x)=](https://math-helper.ru/wp-content/plugins/latex/cache/tex_d10aa71cec83b45d97cc6b0c33f96405.gif)








