Пример 4. Исследовать функцию 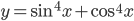 и построить ее график.
и построить ее график.
Решение. I, II. Функция 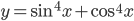 определена и непрерывна на всей числовой оси.
определена и непрерывна на всей числовой оси.
III. Функция является четной, так как  , и периодической, так как
, и периодической, так как 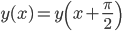 , с периодом
, с периодом  . Достаточно исследовать поведение этой функции и построить ее график в интервале
. Достаточно исследовать поведение этой функции и построить ее график в интервале 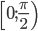 ; в остальных точках числовой оси поведение функции и ее график будут повторяться.
; в остальных точках числовой оси поведение функции и ее график будут повторяться.
IV. При 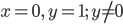 . График функции пересекает ось
. График функции пересекает ось  в точке (0; 1) и не пересекает ось
в точке (0; 1) и не пересекает ось  . При любом значении
. При любом значении  функция имеет положительное значение.
функция имеет положительное значение.
V. а) График функции не имеет вертикальных асимптот, поскольку она непрерывна на всей числовой оси;
б) 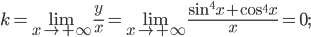
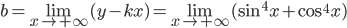 — не существует.
— не существует.
При 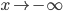 невертикальной асимптоты также не существует.
невертикальной асимптоты также не существует.
График функции не имеет никаких асимптот.
VI. 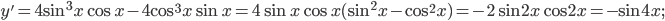
 обращается в нуль в интервале
обращается в нуль в интервале 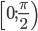 в точках
в точках  и
и 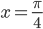 , которые являются критическими. Других критических точек в интервале
, которые являются критическими. Других критических точек в интервале 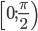 нет, так как
нет, так как  существует всюду.
существует всюду.
Исследуем критические точки по знаку  (по правилу IIб):
(по правилу IIб): 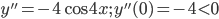 , следовательно,
, следовательно,  есть точка максимума, где , поэтому
есть точка максимума, где , поэтому 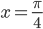 есть точка минимума, где
есть точка минимума, где 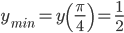 .
.
В интервале 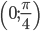 , где
, где  , функция убывает, а в интервале
, функция убывает, а в интервале 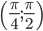 , где , функция возрастает.
, где , функция возрастает.
VII. 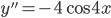 ;
;  существует всюду и обращается в нуль в интервале
существует всюду и обращается в нуль в интервале 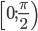 при
при 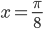 и
и 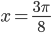 . Эти точки оси
. Эти точки оси  могут быть абсциссами точек перегиба. Исследуя их по знаку
могут быть абсциссами точек перегиба. Исследуя их по знаку  в соседних точках,
в соседних точках,
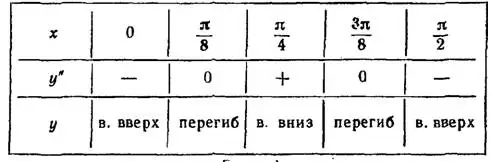
заключаем, что в интервале 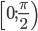 график функции имеет две точки перегиба:
график функции имеет две точки перегиба: 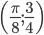 и
и 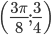 .
.
Ординаты этих точек вычислены из данного уравнения. В интервалах 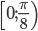 и
и 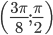 , где
, где  , график функции обращен выпуклостью вверх, а в интервале
, график функции обращен выпуклостью вверх, а в интервале 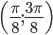 , где , он обращен выпуклостью вниз.
, где , он обращен выпуклостью вниз.
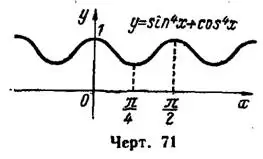
VIII. Согласно полученным результатам исследования строим график функции в интервале 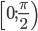 , длина которого равна периоду данной функции, и затем повторяем его влево и вправо по периодическому закону (рис. 71).
, длина которого равна периоду данной функции, и затем повторяем его влево и вправо по периодическому закону (рис. 71).
Пример 5. Исследовать функцию 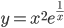 и построить ее график.
и построить ее график.
Решение. I. Функция 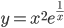 определена на всей числовой оси, кроме точки
определена на всей числовой оси, кроме точки  .
.
II. В точке  функция имеет разрыв: она определена вблизи этой точки, но не определена в самой точке
функция имеет разрыв: она определена вблизи этой точки, но не определена в самой точке
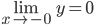 , ибо
, ибо 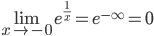 .
.
При 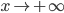 имеет место случай нахождения предела
имеет место случай нахождения предела  . Преобразуя функцию к виду дроби и дважды применяя правило Лопиталя, получим
. Преобразуя функцию к виду дроби и дважды применяя правило Лопиталя, получим
 .
.
Следовательно, в точке  разрыв функции бесконечный. В остальных точках числовой оси она непрерывна.
разрыв функции бесконечный. В остальных точках числовой оси она непрерывна.
III. Функция не является ни четной, ни нечетной, ни периодической.
IV. С осями координат график функции не пересекается; согласно п. II исследования начало координат является предельной точкой левой ветви графика.
Определяя знак функции в какой-либо точке слева от точки разрыва, например , и в какой-либо точке справа от нее, например , заключаем, что функция имеет положительные значения во всей своей области определения.
V. а) Вертикальной асимптотой графика функции является прямая  , ибо при
, ибо при  функция имеет бесконечный разрыв;
функция имеет бесконечный разрыв;
б) 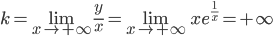 , так как
, так как 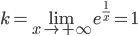 .
.
При 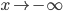 угловой коэффициент невертикальной асимптоты также не существует, т. е. таких асимптот график функции не имеет.
угловой коэффициент невертикальной асимптоты также не существует, т. е. таких асимптот график функции не имеет.
VI. 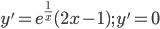 в точке
в точке 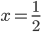 , которая является критической;
, которая является критической;  не существует в точке
не существует в точке  но она не является критической, так как это точка разрыва.
но она не является критической, так как это точка разрыва.
Исследуя критическую точку по знаку  в этой точке:
в этой точке:
заключаем, что
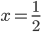 есть точка минимума:
есть точка минимума: 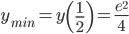 .
.Определяя знак
 в интервалах, границами которых являются точки разрыва и экстремума, заключаем: в интервалах
в интервалах, границами которых являются точки разрыва и экстремума, заключаем: в интервалах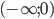 и
и 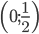 , где
, где  , функция убывает, а в интервале
, функция убывает, а в интервале 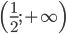 , где , она возрастает.
, где , она возрастает.VII.
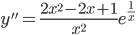 нигде не обращается в нуль и существует во всей области определения функции. Поэтому график функции не имеет точек перегиба.
нигде не обращается в нуль и существует во всей области определения функции. Поэтому график функции не имеет точек перегиба.Определяя знак
 в какой-либо точке слева от точки разрыва, например , и в какой-либо точке справа от нее, например , заключаем, что график функции всюду обращен выпуклостью вниз.
в какой-либо точке слева от точки разрыва, например , и в какой-либо точке справа от нее, например , заключаем, что график функции всюду обращен выпуклостью вниз.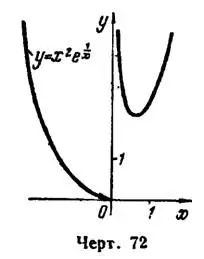
VIII. Ввиду недостаточности полученных данных находим дополнительно несколько точек графика, беря подходящие значения
 и определяя соответствующие значения
и определяя соответствующие значения  из данного уравнения:
из данного уравнения: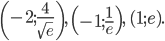
Наконец, строим график функции (рис. 72).







