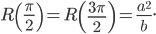Если плоская линия отнесена к прямоугольной системе координат и задана уравнением  или уравнениями
или уравнениями 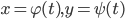 , то ее кривизна
, то ее кривизна 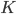 в любой точке определяется формулой
в любой точке определяется формулой
![\displaystyle K=\frac{\left | y'' \right |}{\left [ 1+(y')^{2}\right ]^{\frac{3}{2}}}=\frac{\left | \dot{x}\ddot{y}-\dot{y}\ddot{x} \right |}{(\dot{x}^{2}+\dot{y}^{2})^{\frac{3}{2}}}, \; \; \; \; (1)](https://math-helper.ru/wp-content/plugins/latex/cache/tex_ccb926d5288bc7fc10b1908902ef4107.gif)
где
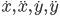 — первая и вторая производные от
— первая и вторая производные от  и
и  по параметру
по параметру  .
.Кривизна линии в некоторой ее точке характеризует отклонение линии от своей касательной в этой точке.
Из всех плоских линий постоянную кривизну имеют только прямая и окружность. У всех других линий кривизна меняется от точки к точке. Кривизна прямой всюду равна нулю; у других линий кривизна может равняться нулю только в отдельных точках. Кривизна окружности радиуса
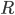 всюду равна
всюду равна 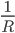 .
.Величина
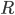 , обратная кривизне кривой в некоторой ее точке
, обратная кривизне кривой в некоторой ее точке 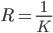 , называется радиусом кривизны кривой в этой точке.
, называется радиусом кривизны кривой в этой точке.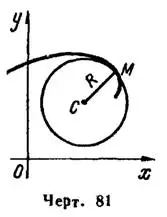
Кругом кривизны кривой в ее точке
 называется окружность с радиусом, равным радиусу кривизны кривой в точке
называется окружность с радиусом, равным радиусу кривизны кривой в точке  , центр которой
, центр которой  лежит на нормали к кривой в точке
лежит на нормали к кривой в точке  со стороны ее вогнутости (рис. 81).
со стороны ее вогнутости (рис. 81).Координаты
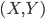 центра кривизны (центра круга кривизны) кривой в ее точке
центра кривизны (центра круга кривизны) кривой в ее точке 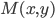 определяются формулами
определяются формулами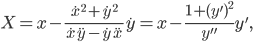
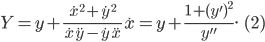
Геометрическое место центров кривизны
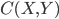 линии называется эволютой этой линии. Уравнения (2) являются параметрическими уравнениями эволюты.
линии называется эволютой этой линии. Уравнения (2) являются параметрическими уравнениями эволюты.Сама кривая по отношению к своей эволюте называется эвольвентой.
Пример 1. Найти кривизну кривой:
1)
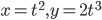 в точке, где
в точке, где 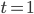 ;
;2)
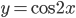 в точке, где
в точке, где 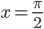 .
.Решение. 1) Находим производные
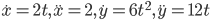 вычисляем их значения в точке, где
вычисляем их значения в точке, где 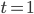 :
: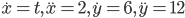
и, подставляя в формулу (1), получим
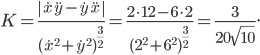
2) Из данного уравнения находим первую и вторую производные от
 по
по  :
: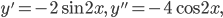
вычисляем их значения в данной точке:
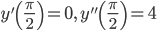 и, подставляя в формулу (1), получим
и, подставляя в формулу (1), получим 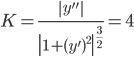 .
.Пример 2. Определить радиусы кривизны в вершинах эллипса
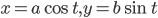 .
.Решение. Найдем производные
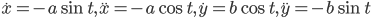 и определим радиус кривизны эллипса в любой его точке:
и определим радиус кривизны эллипса в любой его точке: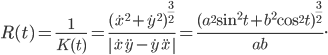
Для вершин эллипса, лежащих на его оси
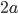 , параметр
, параметр  равен 0 или
равен 0 или  . Поэтому радиус кривизны эллипса в этих вершинах
. Поэтому радиус кривизны эллипса в этих вершинах 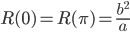 .
.В двух других вершинах эллипса, лежащих на оси
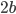 ,
,  или
или 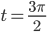 . В этих вершинах радиус кривизны эллипса
. В этих вершинах радиус кривизны эллипса