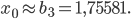Пример 2. Вычислить с точностью до 0,0001 наибольший корень уравнения 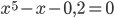 .
.
Решение. Вначале отделим искомый корень графическим методом. Преобразуя уравнение к виду 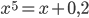 и построив кривые
и построив кривые 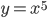 и
и 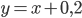 в одних координатных осях (рис. 79), при указанных неодинаковых по осям, но одинаковых для обеих кривых единицах масштаба, заключаем, что искомый наибольший корень содержится на отрезке [1; 1,1].
в одних координатных осях (рис. 79), при указанных неодинаковых по осям, но одинаковых для обеих кривых единицах масштаба, заключаем, что искомый наибольший корень содержится на отрезке [1; 1,1].
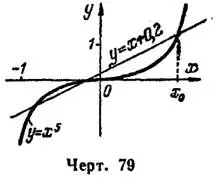
Далее вычислим приближенное значение корня с заданной точностью, пользуясь методом хорд и касательных, т, е. применяя формулы (*), сужающие отрезок, заключающий в себе этот корень.
Однако, прежде чем применять эти формулы, следует убедиться в том, что функция 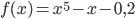 и найденный отрезок [1; 1,1] удовлетворяют необходимым условиям, т. е. что:
и найденный отрезок [1; 1,1] удовлетворяют необходимым условиям, т. е. что:
а) значения функции  на концах отрезка имеют разные знаки и что
на концах отрезка имеют разные знаки и что
б) первая и вторая производные от функции на этом отрезке сохраняют каждая свой знак:
а)
б)
для всех значений х на отрезке [1; 1,1].
Так как  имеет тот же знак, что и
имеет тот же знак, что и 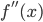 при
при 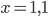 то, обозначив концы отрезка
то, обозначив концы отрезка 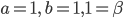 и применяя формулы (*), получим:
и применяя формулы (*), получим:
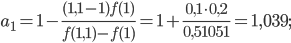
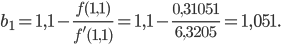
К полученным новым границам
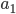 и
и  более узкого отрезка, содержащего искомый корень, применяем те же формулы (*):
более узкого отрезка, содержащего искомый корень, применяем те же формулы (*):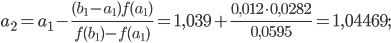
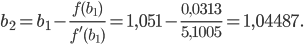
Длина полученного отрезка
![\left [ a_{2};b_{2} \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_8856f421b74849be222e1cc8c3f1d69b.gif) меньше
меньше 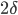 , но больше
, но больше  :
: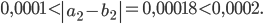
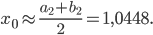
Пример 3. Вычислить с точностью до 0,000001 действительный корень уравнения
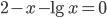 .
.Решение. Чтобы отделить искомый корень, преобразуем уравнение к виду
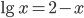 и построим кривые
и построим кривые 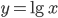 и
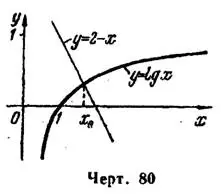
и 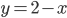 (рис. 80). По чертежу определяем, что искомый корень содержится внутри отрезка [1,6; 1,8].
(рис. 80). По чертежу определяем, что искомый корень содержится внутри отрезка [1,6; 1,8].Для проверки условий, соблюдение которых необходимо при пользовании методом хорд и касательных, вычисляем значения функции
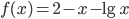 на концах найденного отрезка и находим производные
на концах найденного отрезка и находим производные 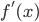 и
и 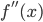 :
:
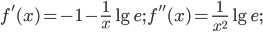
Убедившись, что на концах отрезка функция
 имеет разные знаки и что на всем этом отрезке производные
имеет разные знаки и что на всем этом отрезке производные 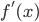 и
и 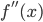 сохраняют каждая свой знак, обозначаем концы отрезка:
сохраняют каждая свой знак, обозначаем концы отрезка: 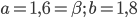 и применяем уточняющие формулы (*):
и применяем уточняющие формулы (*):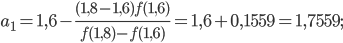
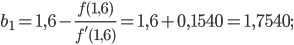
Повторно применяем формулы (*) до тех пор, пока не получим отрезок
![\left [ b_{n};a_{n} \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_4f5ec221cd06acdb6e6d06eaef2f9b4a.gif) , длина которого будет удовлетворять одному из условий (**):
, длина которого будет удовлетворять одному из условий (**):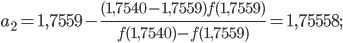
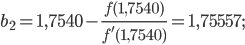
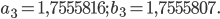
Здесь длина отрезка
![\left [ b_{3};a_{3} \right ]](https://math-helper.ru/wp-content/plugins/latex/cache/tex_090ae93790517523da3d3d35f47fd720.gif) менее 0,000001;
менее 0,000001; 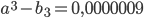 . Поэтому искомое приближенное значение корня данного уравнения с точностью до 0,000001
. Поэтому искомое приближенное значение корня данного уравнения с точностью до 0,000001