Логарифмическое дифференцирование. Практикум по математическому анализу. Урок 31

Дифференцирование многих функций значительно упрощается, если их предварительно прологарифмировать.
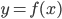Если требуется найти $\displaystyle y'$ из уравнения $\displaystyle y=f(x)$, то можно:
а) логарифмировать обе части уравнения (по основанию /(e/));
$\displaystyle \ln y=\ln f(x)=\varphi (x);$
б) дифференцировать обе части полученного равенства, где $\displaystyle \ln y$ есть сложная функция от /(x/),
$\displaystyle \frac{y'}{y}=\varphi '(x)$ (согласно формуле 11);
в) заменить $y$ его выражением через $\displaystyle x$ и определить $\displaystyle y'$:
$\displaystyle y'=y\varphi '(x)=f(x)\varphi '(x).$
Логарифмическое дифференцирование полезно применять, когда заданная функция содержит логарифмирующиеся операции (умножение, деление, возведение в степень, извлечение корня) и, в частности, для нахождения производной от показательно-степенной функции $\displaystyle y=u^{v}$, где $u$ и $v$ — функции от $x$.
Пример 1. Найти производные следующих функций:
1) $\displaystyle y=x^{x}$;
2) $\displaystyle r=(\cos \alpha )^{\sin 2\alpha };$
3) $\displaystyle s=\frac{2t}{\sqrt{1-t^{2}}}$;
4) $\displaystyle R=(x-1)\sqrt[3]{(x+1)^{2}(x-2)}.$
Решение. Применяя логарифмическое дифференцирование, последовательно находим:
1) а) $\displaystyle \ln y=x\ln x$;
б) $\displaystyle \frac{y'}{y}=x'\ln x+x(\ln x)'=\ln x+x\cdot \frac{1}{x}=\ln x+1;$$
в) $\displaystyle y'=y(1+\ln x)=x^{x}(1+\ln x).$
2) a) $\displaystyle \ln r=\sin 2\alpha \ln \cos \alpha ;$
б) $\displaystyle \frac{r'}{r}=(\sin 2\alpha )'\ln \cos \alpha +\sin 2\alpha (\ln \cos \alpha )'=2\cos 2\alpha \ln \cos \alpha +\sin 2\alpha \left ( -\frac{\sin \alpha }{\cos \alpha } \right )=$
$=2\cos 2\alpha \ln \cos \alpha -2\sin ^{2}\alpha$;
в) $\displaystyle r'=2(\cos 2\alpha \ln \cos \alpha -\sin ^{2}\alpha )(\cos \alpha )^{\sin 2\alpha }$.
3) a) $\displaystyle \ln s=\ln 2+\ln t-\frac{1}{2}\ln (1-t^{2})$;
б) $\displaystyle \frac{s'}{s}=\frac{1}{t}-\frac{1}{2}\cdot \frac{-2t}{1-t^{2}}=\frac{1}{t}+\frac{t}{1-t^{2}}=\frac{1}{t(1-t^{2})};$
в) $\displaystyle s'=\frac{s}{t(1-t^{2})}=\frac{2t}{t(1-t^{2})\sqrt{1-t^{2}}}=\frac{2}{\sqrt{(1-t^{2})^{3}}}.$
4) a) $\displaystyle \ln R=\ln (x-1)+\frac{2}{3}\ln (x+1)+\frac{1}{3}\ln (x-2);$
б) $\displaystyle \frac{R'}{R}=\frac{1}{x-1}+\frac{2}{3(x+1)}+\frac{1}{3(x-2)}=\frac{2x^{2}-3x-1}{(x^{2}-1)(x-2)};$
в) $\displaystyle R'=\frac{2x^{2}-3x-1}{(x^{2}-1)(x-2)}(x-1)\sqrt[3]{(x+1)^{2}(x-2)}=\frac{2x^{2}-3x-1}{\sqrt[3]{(x+1)(x-2)^{2}}}.$