Общие формулы и их частные виды:
12)  13)  14)  15)  | 12а)  13а)  14а)  15а)  |
Пример 1. Найти производные следующих функции:
1) 
2) 
3)  . Найти
. Найти  и
и  .
.
Решение. 1) По формулам 12 и 13 найдем

2) Используя формулы 12 и 15, имеем

так как  равен не
равен не  , а
, а  и
и  .
.
3) Применяем формулы 14 и 15;

Подставляя вместо  заданные значения
заданные значения 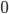 и
и 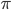 , найдем
, найдем








