Если  есть производная от функции
есть производная от функции 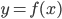 , то производная от
, то производная от  называется второй производной, или производной второго порядка от первоначальной функции
называется второй производной, или производной второго порядка от первоначальной функции  , и обозначается
, и обозначается  или
или  , или
, или  .
.
Аналогично определяются и обозначаются производные любого порядка:
- производная третьего порядка  ;
;
- производная четвертого порядка  ;
;
- производная  -го порядка
-го порядка  .
.
Для нахождения производной какого-либо высшего порядка от данной функции приходится последовательно находить все ее производные низших порядков.
Для произведения двух функций можно получить производную любого  -го порядка, пользуясь формулой Лейбница:
-го порядка, пользуясь формулой Лейбница:

 .
.
Пример 1. Для данных функций найти производные указанного порядка:
1)  . Найти
. Найти  .
.
2)  . Найти
. Найти  .
.
3)  . Найти
. Найти  .
.
4)  ; показать, что функция удовлетворяет уравнению
; показать, что функция удовлетворяет уравнению  .
.
5)  . Найти
. Найти  .
.
6)  . Найти
. Найти  .
.
Решение. 1) Дифференцируя функцию  , получим
, получим
 .
.
Дифференцируя производную  , получим
, получим
 .
.
Дифференцируя вторую производную  , получим
, получим
 .
.
2) 
Для нахождения следующих производных здесь полезно ввести отрицательный показатель степени:
 .
.
3) 
При 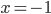 найдем
найдем 
4) Найдем  и
и  :
:

 .
.
Подставляя  в данное уравнение, получим тождество:
в данное уравнение, получим тождество:

5) Применяя формулу Лейбница, получим
![\displaystyle y^{(24)}=\left [ e^{x}(x^{2}-1) \right ]^{(24)}=(e^{x})^{(24)}(x^{2}-1)+24(e^{x})^{(23)}(x^{2}-1)'+](https://math-helper.ru/wp-content/plugins/latex/cache/tex_f2154c410830f87730481e05b4a80cb1.gif)

Все следующие слагаемые равны нулю, ибо все высшие производные от функции  , начиная с третьей, тождественно равны нулю
, начиная с третьей, тождественно равны нулю

(так как производная любого порядка от  есть
есть  ).
).
6) Дифференцируя 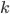 раз, получим:
раз, получим:

В частности, если 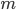 — целое положительное число, то
— целое положительное число, то
 ! и
! и 







