Производные неявной функции. Практикум по математическому анализу. Урок 33

Если у есть неявная функция от $x$, т. е. задана уравнением $\displaystyle f(x,y)=0$, не разрешенным относительно $y$, то для нахождения производной $\displaystyle \frac{dy}{dx}$ нужно продифференцировать по $x$ обе части равенства, помня, что $y$ есть функция от $x$ и затем разрешить полученное равенство относительно искомой производной. Как правило, она будет зависеть от $x$ и $y$; $\displaystyle \frac{dy}{dx}=\varphi (x,y)$.
Вторую производную $\displaystyle \frac{d^{2}y}{dx^{2}}$ от неявной функции получим, дифференцируя функцию $\displaystyle \varphi (x,y)$ по переменной $x$ и помня при этом, что $y$ есть функция от $x$:

$$\displaystyle \frac{d^{2}y}{dx^{2}}=\frac{d\varphi (x,y)}{dx}=F(x,y,\frac{dy}{dx}).$$

Заменяя здесь $\displaystyle \frac{dy}{dx}$ через $\displaystyle \varphi (x,y)$ получим выражение второй производной через $x$ и $y$:

$$\displaystyle \frac{d^{2}y}{dx^{2}}=F\left [ x,y,\varphi (x,y) \right ]=\psi (x,y).$$

Совершенно так же и все высшие производные от неявной функции можно выразить только через $x$ и $y$: каждый раз, когда при дифференцировании появляется производная $\displaystyle \frac{dy}{dx}$, ее следует заменять через $\displaystyle \varphi (x,y)$.
К тому же результату приводит последовательное дифференцирование равенства $\displaystyle f(x,y)=0$ с последующим исключением из полученной системы всех производных низшего порядка.
Пример 1. Для данных неявных функций найти производные указанного порядка.
1) $\displaystyle \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1$. Найти $\displaystyle \frac{dy}{dx}$.
2) $\displaystyle e^{\varphi -2}+r\varphi -3r-2=0$. Найти $\displaystyle \left ( \frac{dr}{d\varphi } \right )_{\varphi =2}$.
3) $\displaystyle x^{y}=y^{x}$. Найти $\displaystyle \frac{dx}{dy}$.
4) $\displaystyle x^{2}+y^{2}-4x-10y+4=0$. Найти $\displaystyle y'_{x=6}$.
Каков геометрический смысл решения этой задачи?
5) $\displaystyle t-s+\textrm{arctg}\: s=0$. Найти $\displaystyle s''$.
6) $\displaystyle y=x+\ln y$. Найти $\displaystyle y''$ и $\displaystyle x''$.
Решение. 1) Дифференцируем по $x$ обе части равенства, где $y$ есть функция от $x$, получим
$\displaystyle \frac{2x}{a^{2}}-\frac{2yy'}{b^{2}}=0$.
Отсюда найдем $\displaystyle y'=\frac{b^{2}x}{a^{2}y}$.
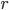2) Дифференцируя по $\displaystyle \varphi$ и считая $r$ функцией $\displaystyle \varphi$, найдем

$$\displaystyle e^{\varphi -2}+\varphi \frac{dr}{d\varphi }+r-3\frac{dr}{d\varphi }=0.$$

Из этого равенства определяем $\displaystyle \frac{dr}{d\varphi }=\frac{e^{\varphi -2}+r}{3-\varphi }.$
Подставляя данное по условию значение $\displaystyle \varphi =2$ в исходное уравнение, найдем соответствующее значение $\displaystyle r_{\varphi =2}=-1$.
Искомое частное значение производной $\displaystyle \frac{dr}{d\varphi }$ при $\displaystyle \varphi =2$ будет
$\displaystyle \left ( \frac{dr}{d\varphi } \right )_{\varphi =2}=\frac{e^{0}-1}{3-2}=0.$
3) Логарифмируем обе части данного уравнения (по основанию $e$), затем дифференцируем по $y$, рассматривая $x$ как функцию $y$:

$$\displaystyle y\ln x=x\ln y;\; y'\ln x+y(\ln x)'=x'\ln y+x(\ln y)';$$

$$\displaystyle 1\cdot \ln x+y\frac{x'}{x}=x'\ln y+x\frac{1}{y}.$$

Отсюда найдем:

$$\displaystyle x'\left ( \frac{y}{x}-\ln y \right )=\frac{x}{y}-\ln x;\; x'=\frac{dx}{dy}=\frac{x(x-y\ln x)}{y(y-x\ln y)}.$$

4) Дифференцируя по $x$, получим $\displaystyle 2x+2yy'-4-10y'=0.$
Отсюда имеем $\displaystyle y'=\frac{x-2}{5-y}$.
Подставляя заданное значение 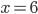$x=6$ в исходное уравнение, найдем два соответствующих ему значения $y$: $\displaystyle y_{1}=2;\: y_{2}=8.$
Поэтому при 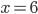$x=6$ и производная $y'$ имеет два значения:

$$\displaystyle y'_{x=6,y=2}=\frac{4}{3};\: y'_{x=6,y=8}=-\frac{4}{3}.$$

Геометрически, в прямоугольной системе координат, заданное в условии задачи уравнение определяет окружность, у которой абсциссу 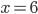$x=6$ имеют две точки: (6; 2) и (6; 8). Найденные значения производной представляют угловые коэффициенты касательных к этой окружности в той и другой точке (рис. 1).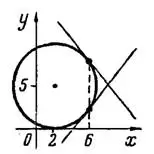

Рис.1

5) 1-й способ. Дифференцируем по $t$ и находим $s'$:

$$\displaystyle 1-s'+\frac{s'}{1+s^{2}}=0;\: s'=\frac{s^{2}+1}{s^{2}}=1+s^{-2}.$$

Последнее равенство снова дифференцируем по $t$ и находим $s''$:

$$\displaystyle s''=-2s^{-3}s'=-\frac{2s'}{s^{3}}.$$

Заменяя здесь $s'$ через $\displaystyle \frac{s^{2}+1}{s^{2}}$, окончательно получим

$$\displaystyle s''=-\frac{2(s^{2}+1)}{s^{5}}.$$

2-й способ. Данное равенство последовательно дифференцируем по $t$ два раза:

$$\displaystyle 1-s'+\frac{s'}{1+s^{2}}=0;\;\;\;(a)$$

$$\displaystyle -s''+\frac{s''(1+s^{2})-2ss's'}{(1+s^{2})^{2}}=0.\;\;\;(b)$$

Из уравнения (a) определяем $s'$ и, подставляя в уравнение (b), получаем соотношение между $t,s$ и $s''$ из которого и выражаем $s''$ через $t$ и $s$. Результат будет тот же, что и при решении 1-м способом.
б) а. Дифференцируем по $x$ и определяем $y''$:

$$\displaystyle y'=1+\frac{y'}{y};\: y'=\frac{y}{y-1}.$$

Дифференцируем последнее равенство по $x$ и определяем $y''$

$$\displaystyle y''=\frac{y'(y-1)-y'y}{(y-1)^{2}}=-\frac{y'}{(y-1)^{2}}.$$

Подставляя вместо $y'$ его значение, имеем $\displaystyle y''=-\frac{y}{(y-1)^{3}}.$
б. Дифференцируем данное равенство по $y$ и определяем $x''$:

$$\displaystyle 1=x'+\frac{1}{y};\: x'=\frac{y-1}{y}.$$

Дифференцируем полученное равенство по $y$ и определяем $x''$:

$$\displaystyle x''=\frac{1\cdot y-1(y-1)}{y^{2}}=\frac{1}{y^{2}}.$$