Непосредственное нахождение производной. Практикум по математическому анализу. Урок 25

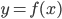Для непосредственного нахождения производной $\displaystyle y'$ от функции $\displaystyle y=f(x)$ служит следующее общее правило.
I. Придаем аргументу $x$ произвольное приращение $\displaystyle \Delta x$ и, подставляя в данное выражение функции вместо $x$ наращенное значение $\displaystyle x+\Delta x$ находим наращенное значение функции:

$$\displaystyle y+\Delta y=f(x+\Delta x)$$

.
II. Вычитая из наращенного значения функции ее первоначальное значение, находим приращение функции

$$\displaystyle \Delta y=f(x+\Delta x)-f(x)$$

.
III. Делим приращение функции на приращение аргумента, т. е. составляем отношение

$$\displaystyle \frac{\Delta y}{\Delta x}=\frac{f(x+\Delta x)-f(x)}{\Delta x}.$$

IV. Ищем предел этого отношения при $\displaystyle \Delta x\rightarrow 0$. Этот предел и даст искомую производную $\displaystyle y'$ от функции $\displaystyle y=f(x)$.
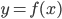Пример 1. Путем вычисления предела $\displaystyle \underset{\Delta x \to 0}{lim}\frac{\Delta y}{\Delta x}$ найти производные следующих функций:
1) $\displaystyle y=3x^{2}-4x$; 2) $\displaystyle y=\frac{1}{x}$; 3) $\displaystyle y=\sqrt{x}$; 4) $\displaystyle y=\cos 3x$.
Решение: Руководствуясь указанным общим правилом для непосредственного нахождения производной, последовательно находим:
1) Для функции $\displaystyle y=3x^{2}-4x$:
I) $\displaystyle y+\Delta y=3(x+\Delta x)^{2}-4(x+\Delta x)=3x^{2}+6x\Delta x+3\Delta x^{2}-4x-4\Delta x;$
II) $\displaystyle \Delta y=(3x^{2}+6x\Delta x+3\Delta x^{2}-4x-4\Delta x)-(3x^{2}-4x)=6x\Delta x+3\Delta x^{2}-4\Delta x;$
III) $\displaystyle \frac{\Delta y}{\Delta x}=\frac{6x\Delta x+3\Delta x^{2}-4\Delta x}{\Delta x}=6x+3\Delta x-4;$
IV) $\displaystyle \underset{\Delta x \to 0}{lim}\frac{\Delta y}{\Delta x}=\underset{\Delta x \to 0}{lim}(6x+3\Delta x-4)=6x-4.$
Следовательно, $\displaystyle \frac{dy}{dx}=\frac{d(3x^{2}-4x)}{dx}=6x-4.$
2) Для функции $\displaystyle y=\frac{1}{x}$:
I) $\displaystyle y+\Delta y=\frac{1}{x+\Delta x};$
II) $\displaystyle \Delta y=\frac{1}{x+\Delta x}-\frac{1}{x}=-\frac{\Delta x}{x(x+\Delta x)};$
III) $\displaystyle \frac{\Delta y}{\Delta x}=-\frac{1}{x(x+\Delta x)};$
IV) $\displaystyle \underset{\Delta x \to 0}{lim}\frac{\Delta y}{\Delta x}=\underset{\Delta x \to 0}{lim}\left ( -\frac{1}{x(x+\Delta x)} \right )=-\frac{1}{x^{2}}.$
Следовательно, $\displaystyle \left ( \frac{1}{x} \right )'=-\frac{1}{x^{2}}.$
3) Для функции $\displaystyle y=\sqrt{x}$:
I) $\displaystyle y+\Delta y=\sqrt{x+\Delta x};$
II) $\displaystyle \Delta y=\sqrt{x+\Delta x}-\sqrt{x};$
III) $\displaystyle \frac{\Delta y}{\Delta x}=\frac{\sqrt{x+\Delta x}-\sqrt{x}}{\Delta x};$
IV) $\displaystyle y'=\underset{\Delta x \to 0}{lim}\frac{\Delta y}{\Delta x}=\underset{\Delta x \to 0}{lim}\frac{\sqrt{x+\Delta x}-\sqrt{x}}{\Delta x}=\underset{\Delta x \to 0}{lim}\frac{x+\Delta x-x}{\Delta x(\sqrt{x+\Delta x}+\sqrt{x})}=\frac{1}{2\sqrt{x}}.$
4) Для функции $\displaystyle y=\cos 3x$:
I) $\displaystyle y+\Delta y=\cos 3(x+\Delta x);$
II) $\displaystyle \Delta y=\cos 3(x+\Delta x)-\cos 3x=-2\sin \left ( 3x+\frac{3}{2}\Delta x \right )\sin \frac{3}{2}\Delta x;$
III) $\displaystyle \frac{\Delta y}{\Delta x}=-\frac{2\sin \left ( 3x+\frac{3}{2}\Delta x \right )\sin \frac{3}{2}\Delta x}{\Delta x};$
IV) $\displaystyle y'= \underset{\Delta x \to 0}{lim}\frac{\Delta y}{\Delta x}=-2\underset{\Delta x \to 0}{lim}\sin \left ( 3x+\frac{3}{2}\Delta x \right )\cdot \underset{\Delta x \to 0}{lim}\frac{\sin \frac{3}{2}\Delta x}{\Delta x}=$
$\displaystyle =-2\sin 3x\cdot \underset{\Delta x \to 0}{lim}\frac{\frac{3}{2}\Delta x}{\Delta x}=-2\sin 3x\cdot\frac{3}{2}=-3\sin 3x.$