Производной функции 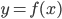 называется предел отношения ее приращения
называется предел отношения ее приращения  к соответствующему приращению
к соответствующему приращению  независимой переменной, когда
независимой переменной, когда  :
:

Производная обозначается
 или
или  , или
, или  .
.Нахождение производной называется дифференцированием.
Геометрически производная
 функции
функции 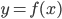 представляет угловой коэффициент касательной к графику этой функции (рис.1):
представляет угловой коэффициент касательной к графику этой функции (рис.1):
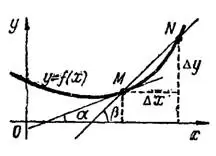
Рис.1
Функция называется дифференцируемой в некоторой точке  , если в этой точке она имеет определенную производную, т. е. если предел (*) существует и имеет одно и то же значение при
, если в этой точке она имеет определенную производную, т. е. если предел (*) существует и имеет одно и то же значение при  любым способом; при этом функция будет и непрерывной в этой точке.
любым способом; при этом функция будет и непрерывной в этой точке.
Непрерывность функции есть необходимое (но недостаточное) условие дифференцируемости функции. Функция, непрерывная в некоторой точке  , может быть и недифференцируемой в этой точке.
, может быть и недифференцируемой в этой точке.
Простейшие случаи недифференцируемости непрерывной функции 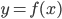 изображены на рис.2.
изображены на рис.2.
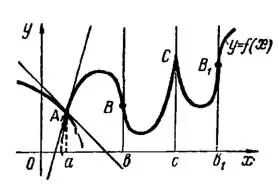
Рис.2
В точке  при
при  отношение
отношение  не имеет предела, но имеет различные односторонние пределы при
не имеет предела, но имеет различные односторонние пределы при  и
и  , которые называются односторонними (левой и правой) производными:
, которые называются односторонними (левой и правой) производными:
 и
и  .
.
В соответствующей точке графика функции нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами:
 и
и  (угловая точка).
(угловая точка).
В точках  и
и  при
при  отношение
отношение  является знакопостоянной бесконечно большой величиной:
является знакопостоянной бесконечно большой величиной:
 (или
(или  ).
).
В этом случае говорят, что функция имеет бесконечную производную. В соответствующих точках график функции имеет вертикальную касательную (точки перегиба с вертикальной касательной).
В точке с односторонние производные являются бесконечно большими величинами разных знаков. В соответствующей точке график функции имеет две слившиеся вертикальные касательные (точка возврата с вертикальной касательной, частный случай угловой точки).
В точках  и
и  функция
функция 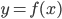 непрерывна, но не дифференцируема.
непрерывна, но не дифференцируема.
Для непосредственного нахождения производной  от функции
от функции 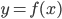 служит следующее общее правило.
служит следующее общее правило.
I. Придаем аргументу  произвольное приращение
произвольное приращение  и, подставляя в данное выражение функции вместо
и, подставляя в данное выражение функции вместо  наращенное значение
наращенное значение  находим наращенное значение функции:
находим наращенное значение функции:

II. Вычитая из наращенного значения функции ее первоначальное значение, находим приращение функции

III. Делим приращение функции на приращение аргумента, т. е. составляем отношение

IV. Ищем предел этого отношения при
 . Этот предел и даст искомую производную
. Этот предел и даст искомую производную  от функции
от функции 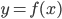 .
.






