Производные простейших алгебраических функций. Практикум по математическому анализу. Урок 26

Понятие производной широко применяется для решения разнообразных задач, однако нет надобности каждый раз находить производную путем предельного перехода, посредством тех четырех операций, которые указаны в общем правиле дифференцирования функций.
Практически производные элементарных функций находятся по формулам дифференцирования, как это разъясняется в последующих задачах.
Таблица производных:

$\displaystyle {(c)}'=0$
2)

$\displaystyle {u+v-w}'={u}'+{v}'-{w}'$
3)

$\displaystyle {uv}'={u}'v+{v}'u$
4)

$\displaystyle {\left ( \frac{u}{v} \right )}'=\frac{{u}'v-{v}'u}{v^{2}}$
4a)

$\displaystyle {\left ( \frac{u}{c} \right )}'=\frac{{u}'}{c}$
4б)

$\displaystyle {\left ( \frac{c}{v} \right )}'=-\frac{c{v}'}{v^{2}}$

$\displaystyle {(x^{n})}'=nx^{n-1}$
6)

$\displaystyle {(\sin x)}'=\cos x$
7)

$\displaystyle {(\cos x)}'=-\sin x$
8)

$\displaystyle {(\textrm{tg} x)}'=\frac{1}{\cos^{2}x}$
9)

$\displaystyle {(\textrm{ctg} x)}'=-\frac{1}{\sin^{2}x}$

где $c$ — постоянная; $x$ — независимая переменная; $\displaystyle u,v,w$ — функции от $x$ .
Пример 1. Пользуясь формулами дифференцирования, найти производные следующих функций:
1) $\displaystyle y=x^{2}-5x+4$ ;
2) $\displaystyle y=\sqrt{x}+\frac{5}{\sqrt[3]{x}}-\frac{1}{x^{2}}+\frac{1}{3x^{3}}$ ;
3) $\displaystyle z=x^{5}\left ( 2-\frac{x}{3}+3x^{2} \right )$ ;
4) $\displaystyle f(x)=\frac{x^{2}}{x^{2}+1}$ .
Решение. 1) $\displaystyle {y}'={(x^{2}-5x+4)}'={(x^{2})}'-{(5x)}'+{(4)}'$ (по формуле 2);
$\displaystyle {y}'=2x-5\cdot 1+0=2x-5$ (по формулам 5, За и 1).
2) Введем дробные и отрицательные показатели, преобразуем данную функцию:
$\displaystyle y=x^{\frac{1}{2}}+5x^{-\frac{1}{3}}-x^{-2}+\frac{1}{3}x^{-8}.$
Применяя формулы 2, 5 и За, получим
$\displaystyle {y}'=\frac{1}{2}x^{-\frac{1}{2}}+5\left ( -\frac{1}{3} \right )x^{-\frac{4}{3}}-(-2)x^{-3}+\frac{1}{3}(-3)x^{-4}=\frac{1}{2\sqrt{x}}-\frac{5}{3\sqrt[3]{x^{4}}}+\frac{2}{x^{3}}-\frac{1}{x^{4}}.$
3) 1-й способ. Пользуясь формулой 3, получим
$\displaystyle {z}'={(x^{5})}'\left ( 2-\frac{x}{3}+3x^{2} \right )+x^{5}\left ( 2-\frac{x}{3}+3x^{2} \right )'=$
$=5x^{4}\left ( 2-\frac{x}{3}+3x^{2} \right )+x^{5}\left ( -\frac{1}{3}+6x \right )=10x^{4}-2x^{5}+21x^{6}.$
2-й способ. Сначала раскроем скобки, затем продифференцируем, как сумму:
$\displaystyle z=2x^{5}-\frac{1}{3}x^{6}+3x^{7};\; z'=10x^{4}-2x^{5}+21x^{6}.$
Этот способ предпочтительнее, так как быстрее приводит к цели.
Следует иметь в виду, что вообще не обязательно дифференцировать заданную функцию сразу. Можно предварительно подвергнуть ее тождественным преобразованиям (если это целесообразно, т. е. ведет к упрощению дифференцирования).
4) Пользуясь формулой 4, получим
$\displaystyle f'(x)=\left ( \frac{x^{2}}{x^{2}+1} \right )'=\frac{(x^{2})'(x^{2}+1)-(x^{2}+1)'x^{2}}{(x^{2}+1)^{2}}=\frac{2x(x^{2}+1)-2x\cdot x^{2}}{(x^{2}+1)^{2}}=\frac{2x}{(x^{2}+1)^{2}}.$

Пример 2. Найти производную данной функции и затем вычислить ее частное значение при указанном значении аргумента:
1) $\displaystyle F(x)=\frac{(1-\sqrt{x})^{2}}{x},\; x=0,01;$
2) $\displaystyle y=\frac{a+b}{3-2x}+\frac{5x^{4}-1}{a-b},\; x=0.$
Решение. 1) Сначала раскроем скобки и выполним деление, затем продифференцируем:
$\displaystyle F(x)=\frac{1-2\sqrt{x}+x}{x}=\frac{1}{x}-\frac{2}{\sqrt{x}}+1=x^{-1}-2x^{-\frac{1}{2}}+1;$
$\displaystyle F'(x)=-x^{-2}-2\left ( -\frac{1}{2} \right )x^{-\frac{3}{2}}=-\frac{1}{x^{2}}+\frac{1}{\sqrt{x^{3}}}.$
Подставляя значение $\displaystyle x=0,01$ , получим
$\displaystyle F'(0,01)=-\frac{1}{0,01^{2}}+\frac{1}{\sqrt{0,01^{3}}}=-100^{2}+10^{3}=-9000.$
2) Применяя формулы 4б и 4а, получим
$\displaystyle y'=-\frac{(a+b)(3-2x)'}{(3-2x)^{2}}+\frac{(5x^{4}-1)'}{a-b}=\frac{2(a+b)}{(3-2x)^{2}}+\frac{20x^{3}}{a-b}.$
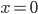При $\displaystyle x=0$ найдем $\displaystyle y'(0)=\frac{2}{9}\left ( a+b \right )$ .