Плоскость в пространстве. Основные формулы

Основные понятия и формулы по теме "Плоскость".
Всякое уравнение первой степени между тремя переменными определяет плоскость. Обратно, всякая плоскость определяется уравнением первой степени относительно текущих координат.
1. Общее уравнение плоскости имеет вид:
Ах + By +Cz + D = 0. (1)
Особые случаи уравнения (1).
а) Пусть в уравнении (1) свободный член D=О, тогда получим уравнение
Ах + By + Сz = 0 (2)
плоскости, проходящей через начало координат.
б) Пусть в уравнении (1) один из коэффициентов А, В и С равен 0.
Тогда получим уравнения плоскостей, параллельных соответствующим координатным осям:
By + Cz + D = 0 — уравнение плоскости, параллельной оси Ох; (3)
Ax + Cz + D = 0 — уравнение плоскости, параллельной оси Оу; (4)
Аx + By + D = 0 — уравнение плоскости, параллельной оси Oz. (5)
в) Пусть в уравнениях (3), (4), (5) свободный член D = 0. Тогда получим уравнения плоскостей, проходящих через соответствующие оси координат:
By + Cz = 0 — уравнение плоскости, проходящей через ось Ох; (6)
Ax + Cz = 0 — уравнение плоскости, проходящей через ось Оу; (7)
Ах + Ву = 0 — уравнение плоскости, проходящей через ось Oz. (8)
г) Пусть в уравнении (1) два коэффициента В = С = 0 или А = С = 0, или А = В = 0. Тогда получим уравнения плоскостей, параллельных соответствующим координатным плоскостям:
Ax + D = 0, или х = а — уравнение плоскости, параллельной координатной плоскости yOz; (9)
By + D = 0, или у = b — уравнение плоскости, параллельной координатной плоскости xOz; (10)
Сz + 0 = 0, или z = c — уравнение плоскости, параллельной координатной плоскости хОу. (11)
д) Пусть в уравнении (1) три коэффициента В, С и D или А, С и D, или A, В и D равны нулю. Тогда получим уравнения координатных плоскостей
Ах = 0, или x = 0 — уравнение плоскости yOz; (12)
Ву = 0, или у = 0 — уравнение плоскости xOz; (13)
Cz = 0, или z = 0 — уравнение плоскости хОу. (14)
2. Общее уравнение плоскости в векторной форме имеет вид:

$$\vec{n}\vec{r}+D=0,\; \; \; (15)$$

$\vec{n}\left\{A,B,C \right\}$ — вектор, перпендикулярный к данной плоскости; $\vec{r}\left\{x,y,z \right\}$ — текущий радиус-вектор.
3. Нормальное уравнение плоскости.
а) Нормальное уравнение плоскости в координатной форме имеет вид:

$$x\cos \alpha +y\cos \beta +z\cos \gamma -p=0.\; \; \; (16)$$

За параметры, определяющие плоскость, приняты: длина перпендикуляра (нормали) р, опущенного из начала координат на плоскость, и направляющие косинусы этого перпендикуляра $\cos \alpha,\: \cos \beta,\: \cos \gamma$.
б) Нормальное уравнение плоскости в векторной форме имеет вид:

$$\vec{n}^{\circ }\vec{r}-p=0,\; \; \; (17)$$

$\vec{n}^{\circ }(\cos \alpha ,\: \cos \beta ,\: \cos \gamma )=\frac{\vec{n}}{n}$ - единичный вектор, перпендикулярный к данной плоскости;
$\cos \alpha,\: \cos \beta,\: \cos \gamma$ — направляющие косинусы вектора; р — расстояние плоскости от начала координат.
4. Для приведения общего уравнения плоскости (1) к нормальному виду (16), нужно умножить его на нормирующий множитель

$$M=\frac{1}{\pm \sqrt{A^{2}+B^{2}+C^{2}}},\; \; \; (18)$$

выбрав знак перед корнем, противоположный знаку свободного члена D в уравнении (1).
Направляющие косинусы и параметр р определяются по формулам:

$$\cos \alpha =\pm \frac{A}{\sqrt{A^{2}+B^{2}+C^{2}}},\; \cos \beta =\pm \frac{B}{\sqrt{A^{2}+B^{2}+C^{2}}},\; \; \; (19)$$

$$\cos \gamma =\pm \frac{C}{\sqrt{A^{2}+B^{2}+C^{2}}},\; p =\pm \frac{D}{\sqrt{A^{2}+B^{2}+C^{2}}}.$$

При этом, если D<0, то берутся верхние знаки; если D>0, то берутся нижние знаки.
5. Уравнение плоскости в отрезках имеет вид:

$$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1,\; \; \; (20)$$

где за параметры, определяющие плоскость, приняты отрезки a, b и с, отсекаемые этой плоскостью на осях координат.
6. Уравнение плоскости, проходящей через данную точку.
а) Уравнение плоскости, проходящей через данную точку, в координатной форме имеет вид:

$$A(x-x_{1})+B(y-y_{1})+C(z-z_{1})=0.\; \; \; (20)$$

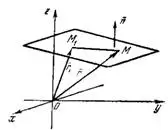
б) Уравнение плоскости, проходящей через данную точку, в векторной форме имеет вид:

$$\vec{n}(\vec{r}-r_{1})=0.\; \; \; (22)$$

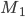$M_{1}$ — данная точка, заданная радиусом-вектором $\vec{r}_{1}\left\{x_{1};y_{1};z_{1} \right\}$,
$\vec{r}\left\{x;y;z \right\}$ — радиус-вектор любой точки плоскости; $\vec{n}\left\{A,B,C \right\}$ — нормальный вектор (рис.1)
7. Угол между двумя плоскостями.
а) Угол между двумя плоскостями, заданными уравнениями в координатной форме

$$\left\{\begin{matrix} A_{1}x+B_{1}y+C_{1}z+D_{1}=0,\\ A_{2}x+B_{2}y+C_{2}z+D_{2}=0, \end{matrix}\right.$$

определяется по формуле:

$$\cos \phi =\frac{A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}}{\sqrt{A_{1}^{2}+B_{1}^{2}+C_{1}^{2}}\cdot \sqrt{A_{2}^{2}+B_{2}^{2}+C_{2}^{2}}}.\; \; \; (23)$$

б) Угол между двумя плоскостями, заданными уравнениями в векторной форме

$$\vec{n}_{1}\vec{r}+D_{1}=0,\; \; \; \vec{n}_{2}\vec{r}+D_{2}=0,\; \; \; (24)$$

где $\vec{n_{1}}\left\{A_{1}, B_{1}, C_{1}\right\},\; \; \; \vec{n_{2}}\left\{A_{2}, B_{2}, C_{2}\right\},$ определяется по формуле

$$\cos \phi =\frac{\vec{n}_{1}\cdot \vec{n}_{2}}{n_{1}n_{2}}.\; \; \; (25)$$

8. Условие параллельности двух плоскостей имеет вид:

$$\frac{A_{1}}{A_{2}}=\frac{B_{1}}{B_{2}}=\frac{C_{1}}{C_{2}}.\; \; \; (26)$$

9. Условие перпендикулярности двух плоскостей имеет вид:

$$A_{1}A_{2}+B_{1}B_{2}+C_{1}C_{2}=0.\; \; \; (27)$$

10. Расстояние от точки до плоскости.
Отклонением данной точки от данной плоскости называется число $\delta$, равное длине перпендикуляра, опущенного из этой точки на плоскость, взятое со знаком плюс, если точка и начало координат лежат по разные стороны от этой плоскости, и со знаком минус, если они лежат по одну сторону от плоскости.
Отклонение $\delta$ получается в результате подстановки координат данной точки в нормальное уравнение данной плоскости

$$\delta =x_{1}\cos \alpha +y_{1}\cos \beta +z_{1}\cos \gamma - p_{1}\; \; \; (28)$$

или в векторной форме

$$\delta =\vec{n^{\circ }}\vec{r}_{1}-p.\; \; \; (29)$$

Расстояние d от точки 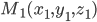$M_{1}(x_{1},y_{1},z_{1})$ до плоскости Ax + By + Cz + D = 0 равно абсолютной величине отклонения:

$$d=\left|x_{1}\cos \alpha +y_{1}\cos \beta +z_{1}\cos \gamma -p \right|,\; \; \; (30)$$

или

$$d=\frac{\left|Ax_{1}+By_{1}+Cz_{1}+D \right|}{\sqrt{A^{2}+B^{2}+C^{2}}};\; \; \; (30')$$

в векторной форме:

$$d=\left|\vec{n^{\circ }}\vec{r_{1}}-p \right|.\; \; \; (30'')$$

11. Уравнение плоскости, проходящей через три данные точки $M_{1}(x_{1},y_{1},z_{1}),\: M_{2}(x_{2},y_{2},z_{1}),\:M_{3}(x_{3},y_{3},z_{3}),$
не лежащие на одной прямой, имеет вид:
а) в координатной форме:

$$\begin{vmatrix} x-x_{1} &y-y_{1} & z-z_{1}\\ x_{2}-x_{1} &y_{2}-y_{1} & z_{2}-z_{1}\\ x_{3}-x_{1} &y_{3}-y_{1} & z_{3}-z_{1} \end{vmatrix}=0\; \; \; (31)$$

б) в векторной форме:

$$\left(\vec{r}-\vec{r_{1}} \right)\left(\vec{r_{2}}-\vec{r_{1}} \right)\left(\vec{r_{3}}-\vec{r_{1}} \right)=0.\; \; \; (31')$$