Решение типовых задач по теме "Плоскость". Часть 1
Задача №1. Построить плоскости, заданные уравнениями:
а) 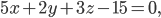 б)
б)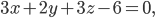 в)
в)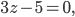
г)  д)
д)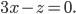
Построение. а) Чтобы построить плоскость, не проходящую через начало координат, необходимо найти отрезки, отсекаемые плоскостью на осях координат. Отрезок, отсекаемый плоскостью на оси Ох, мы найдем, если в уравнении плоскости положим у=0 и z=0; тогда 5х—15=0, а=х=3; аналогично, если x=0 и z=0, то 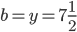 ; если х = 0; y=0, то c=z=5.
; если х = 0; y=0, то c=z=5.
Отложив на координатных осях отрезки а=3, b=7,5 и с=5, соединяем полученные точки М, N, Р прямыми линиями. Эти прямые — следы данной плоскости на координатных плоскостях (рис.1).
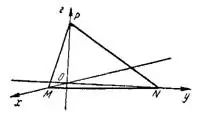
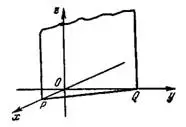
б) Так как уравнение плоскости Зх+2y-6 0 не содержит члена с координатой z (с=0), то плоскость параллельна оси Oz. Следовательно, плоскость отсекает на осях Ох и Оу отрезки а и b конечной величины, а на оси Oz — отрезок с бесконечно большой величины.
Найдем отрезки а и b вышеуказанным способом: а=2, b=3. Отложив эти отрезки на осях Ох и Оу, соединив их концы, получим след плоскости в плоскости хОу. Следы данной плоскости в координатных плоскостях xOz и yOz будут параллельны оси Oz (рис.2).
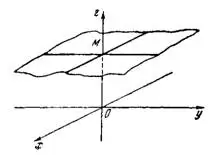
в) Так как в уравнении Зz-5=0 коэффициенты A=0 и В=0, то плоскость, одновременно параллельная оси Ох и оси Оу, параллельна плоскости хОу. Она отсекает на оси Oz отрезок с, равный  . Следы данной плоскости в координатных плоскостях хOz и yOz параллельны соответственно осям Ох и Оу (рис.3).
. Следы данной плоскости в координатных плоскостях хOz и yOz параллельны соответственно осям Ох и Оу (рис.3).
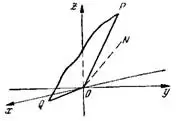
г) Плоскость, заданная уравнением  , проходит через начало координат, следовательно, она не отсекает отрезков на осях координат. Будем строить плоскость путем непосредственного нахождения следов плоскости на координатных плоскостях. Следами плоскости на координатных плоскостях являются прямые. Чтобы найти уравнения этих прямых, в уравнении плоскости будем последовательно полагать х=0, у=0, z=0. Получим след плоскости на yOz:
, проходит через начало координат, следовательно, она не отсекает отрезков на осях координат. Будем строить плоскость путем непосредственного нахождения следов плоскости на координатных плоскостях. Следами плоскости на координатных плоскостях являются прямые. Чтобы найти уравнения этих прямых, в уравнении плоскости будем последовательно полагать х=0, у=0, z=0. Получим след плоскости на yOz:
х=0, — 4у+2z=0, или 
на xOz: 
на хОу: 
Строим полученные прямые в соответствующей координатной плоскости.
Следом данной плоскости в плоскости yOz является прямая ОР; в плоскости xOz — прямая ON; в плоскости хОу — прямая OQ. Следы ОР и OQ —видимые, а след ON невидимый, так как его закрывает плоскость yOz (рис.4).
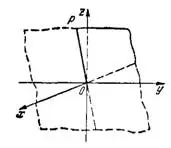
д) В уравнении 3x-z=0 коэффициент B=0 и свободный член D=0, следовательно, плоскость проходит через ось Оу.
Следом данной плоскости в плоскости xOz является прямая Зх-z=0 (прямая ОР). Следы в плоскостях хОу и yOz совпадают с осью Оу (рис.5).
Решение этой задачи также изложено в следующем видео:







