Решение типовых задач по теме "Плоскость". Уравнение плоскости. Часть 1

Решение типовых задач по теме "Плоскость". Составить уравнение плоскости
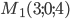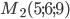Задача №1. Даны точки $M_{1}(3;0;4)$ и $M_{2}(5;6;9)$. Написать уравнение плоскости, проходящей через точку 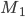$M_{1}$ и перпендикулярно к вектору $M_{1}M_{2}$.
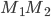Решение. Уравнение связки плоскостей, проходящей через точку 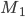$M_{1}$, будет

$$A(x-3)+B(y-0)+C(z-4)=0.$$

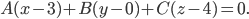
Нормальный вектор

$$\vec{M_{1}M_{2}}=(5-3)\vec{i}+(6-0)\vec{j}+(9-4)\vec{k}=2\vec{i}+6\vec{j}+5\vec{k}.$$

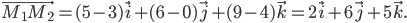
Подставляем проекции 2, 6 и 5 вектора 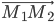$\vec{M_{1}M_{2}}$ на место A, В и С в уравнение связки, будем иметь: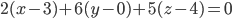

$$2(x-3)+6(y-0)+5(z-4)=0$$

или

$$2x+6y+5z-26=0.$$

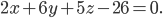
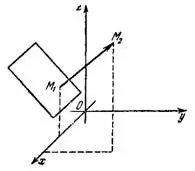
Это и есть уравнение искомой плоскости (рис.1).

Ответ: 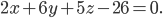$2x+6y+5z-26=0.$
Задача №2. Написать уравнение плоскости, проходящей через точки 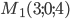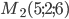$M_{1}(3;0;4)$, $M_{2}(5;2;6)$ и $M_{3}(2;3;-3)$.
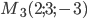Решения задач №1 и №2 подробно изложены в следующем видео

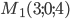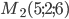Задача №3. Написать уравнение плоскости, проходящей через точки $M_{1}(3;0;4)$ и $M_{2}(5;2;6)$ и перпендикулярной к плоскости 2x+4y+6z-7=0.
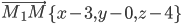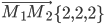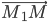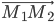Решение. Пусть М(х,у,z) произвольная точка искомой плоскости. Тогда векторы $\vec{M_{1}M}\left\{x-3,y-0,z-4 \right\}$ и $\vec{M_{1}M_{2}}\left\{2,2,2 \right\}$ принадлежат этой плоскости. Векторы $\vec{M_{1}M}$ и $\vec{M_{1}M_{2}}$ компланарны с нормальным вектором 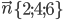$\vec{n}\left\{2;4;6 \right\}$ данной плоскости 2х+4y+бz-7=0.
Поэтому смешанное произведение этих трех векторов равно нулю: 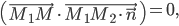$\left(\vec{M_{1}M}\cdot \vec{M_{1}M_{2}\cdot \vec{n}} \right)=0,$
или

$$\begin{vmatrix} x-3 & y-0 &z-4 \\ 2 &2 & 2\\ 2 & 4 & 6 \end{vmatrix}=0.$$

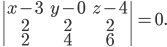
Раскрывая определитель, получаем искомое уравнение плоскости: х-2у-z-7=0.
Ответ: х-2у-z-7=0.
Задача №4. Написать уравнение плоскости, проходящей через точку 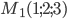$M_{1}(1;2;3)$ и перпендикулярной к плоскостям x-y+z-7=0 и Зх+2у-12z+5 = 0.
Решения задач №3 и №4 подробно изложено в следующем видео

Задача №5. Составить уравнение плоскости, если ее расстояние от начала координат равно 10 и вектор 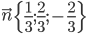$\vec{n}\left\{\frac{1}{3};\frac{2}{3};-\frac{2}{3} \right\}$ перпендикулярен к плоскости и направлен к ней от начала координат.
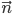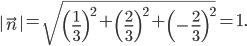
Решение. Вычисляем длину вектора $\vec{n}$:
$\left|\vec{n} \right|=\sqrt{\left(\frac{1}{3} \right)^{2}+\left(\frac{2}{3} \right)^{2}+\left(-\frac{2}{3} \right)^{2}}=1.$
Таким образом, вектор 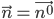$\vec{n}=\vec{n^{0}}$ — единичный. Тогда нормальное уравнение искомой плоскости в векторной форме будет: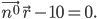 $\vec{n^{0}}\vec{r}-10=0.$
Нормальное уравнение этой же плоскости в координатной форме будет иметь вид:

$$\frac{1}{3}x+\frac{2}{3}y-\frac{2}{3}z-10=0.$$

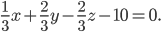
Ответ: $\vec{n^{0}}\vec{r}-10=0,$ $\frac{1}{3}x+\frac{2}{3}y-\frac{2}{3}z-10=0.$
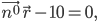
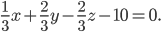
Задача №6. Привести к нормальному виду уравнение плоскости: $\left(10\vec{i}+2\vec{j}-11\vec{k} \right)\vec{r}+60=0.$
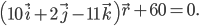
Решения задач №5 и №6 подробно изложены в следующем видео