Решение типовых задач по теме "Плоскость". Часть 2

Решение типовых задач по теме "Задание плоскости в пространстве". Часть 2
Задача №1. Определить направляющие косинусы вектора, направленного из начала координат перпендикулярно к плоскости x-2y+2z-9=0.
Решение. Приводим уравнение плоскости к нормальному виду. Нормирующий множитель:

$$M=\frac{1}{\sqrt{1^{2}+(-2)^{2}+2^{2}}}=\frac{1}{\sqrt{9}}=\frac{1}{3}.$$

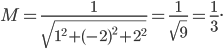
Умножая данное уравнение на 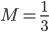$M=\frac{1}{3}$, получим нормальное уравнение плоскости: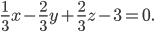

$$\frac{1}{3}x-\frac{2}{3}y+\frac{2}{3}z-3=0.$$

Здесь $\cos \alpha =\frac{1}{3},\; \cos \beta =-\frac{2}{3},\; \cos \gamma =\frac{2}{3}$
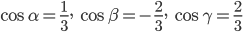
суть направляющие косинусы нормального вектора

$$\vec{n}\left\{A;B;C \right\}=\vec{n}\left\{1;-2;2 \right\}$$

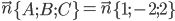
данной плоскости.
Ответ: $\vec{n}\left\{1;-2;2 \right\}$.
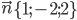Задача №2. Найти расстояние плоскости 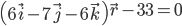$\left(6\vec{i}-7\vec{j}-6\vec{k} \right)\vec{r}-33=0$ от начала координат и углы, которые образует с осями координат перпендикуляр, опущенный из начала координат на плоскость.
Решения задач №1 и №2 подробно изложены в следующем видео

Задача №3. Уравнение плоскости 11х-7у-9z+15=0 написать в векторной форме в общем и в нормальном видах.
Задача №4. Составить уравнение плоскости, перпендикулярной к вектору 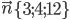$\vec{n}\left\{3;4;12 \right\}$ и отстоящей от начала координат на расстояние р=3.
Решение. Уравнение плоскости, параллельной искомой и проходящей через начало координат, имеет вид: Зх+4у+12z=0.
Отклонение любой точки М(х;у;z) искомой плоскости Зх+4у+12z=0 равно ±3.
Тогда, воспользовавшись формулой

$$\delta =\frac{Ax_{1}+By_{1}+Cz_{1}+D}{\sqrt{A^{2}+B^{2}+C^{2}}},$$

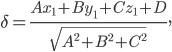
будем иметь:

$$\pm 3 =\frac{3x+4y+12z}{\sqrt{3^{2}+4^{2}+12^{2}}},\; \pm 3 =\frac{3x+4y+12z}{13}.$$

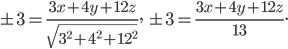
Откуда Зх+4у+12z±39=0 — искомые уравнения плоскости.
Ответ: Зх+4у+12z±39=0.
Решения задач №3 и №4 подробно изложены в следующем видео

Задача №5. Через точки М(3;-2;1) и N(0;3;5) провести плоскость, которая отсекала бы на осях Ох и Оу равные положительные отрезки.
Задача №6. Найти направляющие косинусы прямой, перпендикулярной к плоскости, которая отсекает на осях координат отрезки а=-18, b=-9, с=9.
Решение. Воспользовавшись уравнением плоскости в отрезках 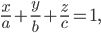$\frac{x}{a}+\frac{y}{b}+\frac{z}{c}=1,$
составим уравнение плоскости: 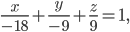$\frac{x}{-18}+\frac{y}{-9}+\frac{z}{9}=1,$
или

Приведем общее уравнение плоскости к нормальному виду: нормирующий множитель

$$M=\frac{1}{\pm \sqrt{A^{2}+B^{2}+C^{2}}}$$

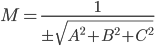
берем со знаком минус, так как в уравнении плоскости D= 18>0:

$$M=\frac{1}{- \sqrt{1+4+4}}=-\frac{1}{3}.$$

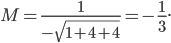
Теперь умножим уравнение (1) на 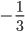$-\frac{1}{3}$. Получим: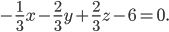

$$-\frac{1}{3}x-\frac{2}{3}y+\frac{2}{3}z-6=0.$$

Направляющие косинусы перпендикуляра к плоскости имеют следующие значения:

$$\cos \alpha =-\frac{1}{3},\; \cos \beta =-\frac{2}{3},\; \cos \gamma =\frac{2}{3}.$$

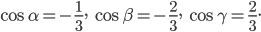
Ответ: $\cos \alpha =-\frac{1}{3},\; \cos \beta =-\frac{2}{3},\; \cos \gamma =\frac{2}{3}.$
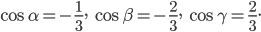
Решения задач №6 и №7 подробно изложены в следующем видео