Решение типовых задач по теме "Плоскость". Часть 3

Решение типовых задач по теме "Задание плоскости в пространстве". Часть 3
Задача №1. Даны две параллельные плоскости 3x + 4y-2z-1=0 и 6x+8y-4z-3=0.
Найти среднюю плоскость (т.е. параллельную данным плоскостям и расположенную между ними на равных расстояниях от них).
Решение. Пусть точка $M(x;y;z)$ принадлежит искомой плоскости. Определим ее отклонение от каждой из данных плоскостей по формуле:

$$\delta =\frac{Ax_{1}+By_{1}+Cz_{1}+D}{\sqrt{A^{2}+B^{2}+C^{2}}}.$$

$$\delta_{1} =\frac{3x+4y-2z-1}{\sqrt{9+16+4}}=\frac{3x+4y-2z-1}{\sqrt{29}}.$$

$$\delta_{2} =\frac{6x+8y-4z-3}{\sqrt{36+64+16}}=\frac{6x+8y-4z-3}{\sqrt{116}}=\frac{6x+8y-4z-3}{2\sqrt{29}}.$$

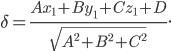
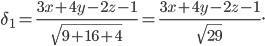
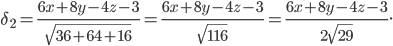
Так как точка М лежит между данными плоскостями, а плоскости расположены по одну сторону от начала координат.
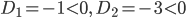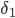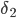$D_{1}=-1<0,\; D_{2}=-3<0$, то отклонения $\delta _{1}$ и $\delta _{2}$ будут противоположных знаков: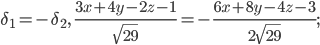

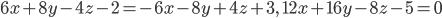$$\delta _{1}=-\delta _{2},\; \frac{3x+4y-2z-1}{\sqrt{29}}=-\frac{6x+8y-4z-3}{2\sqrt{29}};$$

$6x+8y-4z-2=-6x-8y+4z+3,\; 12x+16y-8z-5=0$ — искомое уравнение.
Ответ: $12x+16y-8z-5=0$.
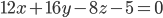Задача №2. Найти плоскость, параллельную двум данным параллельным плоскостям
2х+3y-z-1=0 и 4x+6y-2z+3=0 и делящую расстояние между ними в отношении 2:3.
Решения задач №1 и №2 подробно изложены в следующем видео

Задача №3. Найти плоскость, проходящую через точку (2;-1;1) перпендикулярно к линии пересечения двух плоскостей: 3x-y-z+1=0, x-y+2z+1=0.
Задача №4. На оси Ох найти точку, равноудаленную от точки М(0;1;-2) и от плоскости бх+Зy-2z-9=0.
Решение. Точка, лежащая на оси Ох, имеет ординату и аппликату, равными 0. Таким образом, искомая точка N(х;0;0). Ее расстояние до точки М: 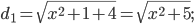$d_{1}=\sqrt{x^{2}+1+4}=\sqrt{x^{2}+5};$
ее расстояние до плоскости:

$$d_{2}=\frac{6x+3\cdot 0-2\cdot 0-9}{\sqrt{36+9+4}}=\frac{6x-9}{7}.$$

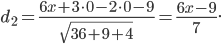
Согласно условию 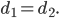$d_{1}=d_{2}.$ Имеем: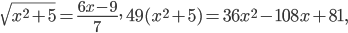

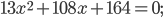
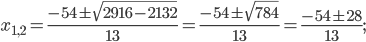
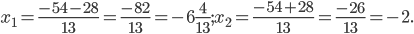
$$\sqrt{x^{2}+5}=\frac{6x-9}{7},\; 49(x^{2}+5)=36x^{2}-108x+81,$$

$$13x^{2}+108x+164=0;$$

$$x_{1,2}=\frac{-54\pm \sqrt{2916-2132}}{13}=\frac{-54\pm \sqrt{784}}{13}=\frac{-54\pm 28}{13};$$

$$x_{1}=\frac{-54-28}{13}=\frac{-82}{13}=-6\frac{4}{13}; x_{2}=\frac{-54+28}{13}=\frac{-26}{13}=-2.$$

Условию удовлетворяют две точки:
Ответ: $N_{1}\left(-6\frac{4}{13};0;0 \right),\; N_{2}\left(-2;0;0 \right).$
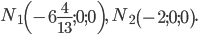
Решения задач №3 и №4 подробно изложены в следующем видео

Задача №5. Найти геометрическое место точек, отклонения которых от плоскости 12x-15y+16z-10=0 равно ±5.
Решение. Возьмем произвольную точку М(x;у;z) и определим ее отклонение до данной плоскости:

$$\delta =\frac{12x-15y+16z-10}{\sqrt{12^{2}+15^{2}+16^{2}}}=\frac{12x-15y+16z-10}{25}.$$

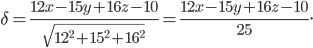
Согласно условию это отклонение равно ±5. Получим два уравнения:

$$\frac{12x-15y+16z-10}{25}=5,\; \frac{12x-15y+16z-10}{25}=-5,$$

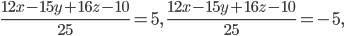
или после упрощения

$$12x-15y+16z-135=0,\; 12x-15y+16z+115=0.$$

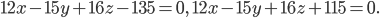
Мы получили две плоскости, параллельные данной плоскости и расположенные по разные стороны от нее на расстоянии 5 единиц.
Ответ: $12x-15y+16z-135=0,\; 12x-15y+16z+115=0.$
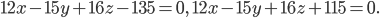
Задача №6. Составить уравнение геометрического места точек, равноудаленных от двух параллельных плоскостей: x-5y+3z+5=0 и 2х-10y+6z+9=0.
Решения задач №3 и №4 подробно изложены в следующем видео

Задача №7. Составить уравнения плоскостей, делящих по¬полам двугранные углы, образованные двумя пересекающимися плоскостями: 5x-2y+5z-3=0 и 2x+y-7z+2=0.
Задача №8. Определить, лежат ли точки М(1;2;-1) и N(-3;1;2) в одном, в смежных или вертикальных двугранных углах, образованных при пересечении двух плоскостей:
1) 2х-3y+z-3=0, х-у-2z+4=0;
2) 5х-2y+z-1=0, 6x-Зу+2z-1=0;
3) 3х+у+ 11z-3=0, 4х+2y-5z+1=0.
Решения задач №5 и №6 подробно изложены в следующем видео

Задача №9. Установить, какие из следующих пар плоскостей пересекаются, параллельны или совпадают:
1) Зх+у-5z-12=0 и 2x+6z-3=0;
2) 2х-Зу+z+8=0 и 4х-6у-Зz-7=0;
3) 5х+2у-3z-5=0 и 10x+4y-6z+5=0;
4) Зx+7y+z+4=0 и 9x+21y+3z+12=0.
Задача №10. Даны уравнения трех граней параллелепипеда x-3y+4z-12=0, y+2z-5=0, x+4=0, и одна из его вершин (4;-3;2). Найти уравнения трех других граней параллелепипеда.
Решения задач №7 и №8 подробно изложены в следующем видео