Решение типовых задач по теме "Плоскость". Пучок плоскостей. Часть 4

Решение типовых задач по теме "Задание плоскости в пространстве". Часть 4
Задача №1. Составить уравнение плоскости, проходящей через линию пересечения плоскостей Зx+y+z-4=0, x+3z-5=0 и отсекающей на осях Ох и Оу равные от­резки.
Решение. Уравнение пучка плоскостей, проходя­щих через линию пересечения двух данных плоскостей, имеет вид:

$$3x+y+z-4+\lambda (x+3z-5)=0,$$

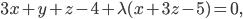
или

$$(3+\lambda )x+y+(1+3\lambda )z-(4+5\lambda)=0.$$

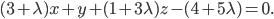
Запишем это уравнение в виде уравнения в отрезках:

$$\frac{(3+\lambda )x}{4+5\lambda }+\frac{y}{4+5\lambda }+\frac{(1+3\lambda )z}{4+5\lambda }=1,$$

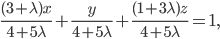
или

$$\frac{x}{\frac{4+5\lambda }{3+\lambda }}+\frac{y}{4+5\lambda }+\frac{z}{\frac{4+5\lambda }{1+3\lambda }}=1.$$

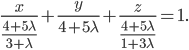
Согласно условию, отрезки, отсекаемые на осях Ох и 0y, равны, т. е.

$$\frac{4+5\lambda }{3+\lambda }=4+5\lambda ,\; 1=3+\lambda ,\; \lambda =-2.$$

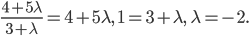
Таким образом, искомым уравнением плоскости яв­ляется уравнение:

$$(3-2)x+y+(1-6)z-(4-10)=0,\; x+y-5z+6=0.$$

Ответ: х+у-5z+6=0.
Задача №2. Из пучка, определяемого плоскостями Зх+у-2z-6=0 и х-2y+5z-1=0 выделить две взаимно перпендикулярные плоскости, из которых одна проходит через точку А(2;-3;4).
Решения задач №1 и №2 подробно изложены в следующем видео

Задача №3. Составить уравнение плоскости, проходящей через точку пересечения трех плоскостей
2x—y-z-1=0, x+2z-4=0, x-y=0, через начало координат и через точку М(7; 1; 2).
Задача №4. На линии пересечения двух плоскостей 2х+y+z+8=0, х-4y-2z-5=0 найти точки, отстоящие от плоскости Зх-6y+2z-10=0 на расстоянии 5 единиц.
Решения задач №3 и №4 подробно изложены в следующем видео

Задача №5. Установить, что три плоскости 2x-4y+5z-21=0, х-3z+18=0, 6х+y+z-30=0 имеют общую точку, и вычислить ее координаты.
Решение. Если определитель $\Delta$ системы

$$\left\{\begin{matrix} 2x-4y+5z=21,\\ x-3z=-18,\\ 6x+y+z=30, \end{matrix}\right.$$

отличен от нуля, то три плоскости, выражаемые данны­ми уравнениями, пересекаются в единственной точке:

$$\Delta =\begin{vmatrix} 2 & -4 & 5\\ 1 & 0 &-3\\ 6 & 1 & 1 \end{vmatrix}=0+5+72-0+6+4=87\neq 0.$$

Плоскости имеют общую точку. Найдем ее:

$$\Delta_{x} =\begin{vmatrix} 21 & -4 & 5\\ -18 & 0 &-3\\ 30 & 1 & 1 \end{vmatrix}=0-90+360-0+63-72=261;$$

$$x=\frac{\Delta _{x}}{\Delta }=\frac{261}{87}=3, \; x=3;\; z=\frac{x+18}{3},$$

$$z=\frac{3+18}{3}=7,\; z=7;\; y=30-6x-z,\; y=30-18-7=5,\; y=5.$$

Ответ: M(3;5;7).
Задача №6. Проверить, имеют ли общую точку следующие четыре плоскости:
а) 2х+2у-3z-9=0, 5х-у+8z-1=0, x+3y+2z-1=0 и Зx+5у-z-10=0;
б) 2х-4y-z+5=0, Зx+5у+4z-3=0, 2у+3z—1=0 и 5x+2y-2=0.
Решения задач №5 и №6 подробно изложены в следующем видео