Поверхности вращения. Основные формулы

Поверхности вращения

Пусть в плоскости yOz дана линия L, имеющая уравнение 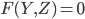$F(Y,Z)=0$. Тогда, чтобы получить уравнение поверхности, образо­ванной вращением линии L, лежащей в плоскости yOz вокруг оси Оу, нужно в уравнении этой линии заменить Z на 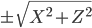$\pm \sqrt{X^{2}+Z^{2}}$. Искомое уравнение поверхности вращения будет:
$F(Y;\sqrt{X^{2}+Z^{2}})=0.\; \; \; (10)$
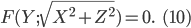
Аналогичные правила будут иметь место и по отношению к по­верхностям, полученным вращением плоских линий вокруг других координатных осей.

Поверхности второго порядка и их канонические уравнения.

1. Сфера. Сферой или шаровой поверхностью называется гео­метрическое место точек пространства, равноудаленных от одной точки, называемой центром сферы.
а) Уравнение сферы имеет вид:

$$(x-a)^{2}+(y-b)^{2}+(z-c)^{2}=r^{2},\; \; \; (11)$$

где а, b и с — координаты центра сферы, а r — ее радиус.
б) Уравнение сферы с центром в начале координат имеет вид:

$$x^{2}+y^{2}+z^{2}=r^{2}.\; \; \; (12)$$

Уравнение второй степени изображает сферу, если коэффици­енты при квадратах координат равны между собой, а члены с про­изведением координат отсутствуют.
Координаты центра и радиус сферы находятся путем приведе­ния уравнения сферы к виду (11).
2. Эллипсоид. Эллипсоидом называется поверхность, канониче­ское (простейшее) уравнение которой имеет вид

$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}+\frac{z^{2}}{c^{2}}=1.\; \; \; (13)$$

(рис.1). Центр эллипсоида лежит в начале координат.

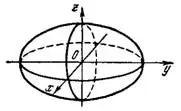
Отрезки а, b и с — называются полуосями эллипсоида.
Если $a=b\neq c$, то уравнение (13) определяет эллипсоид вращения

$$\frac{x^{2}+y^{2}}{a^{2}}+\frac{z^{2}}{c^{2}}=1.\; \; \; (13')$$

3. Гиперболоиды
а) Однополостный гиперболоид.
Однополостным гиперболоидом называется поверхность, канони­ческое (простейшее) уравнение которой имеет вид:

$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=1.\; \; \; (14)$$

(рис.2).
При a=b уравнение (14) определяет однополостный гипербо­лоид вращения.

$$\frac{x^{2}+y^{2}}{a^{2}}-\frac{z^{2}}{c^{2}}=1.\; \; \; (14')$$

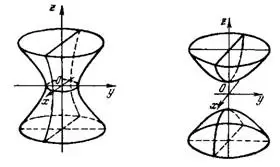
б) Двухполостный гиперболоид.
Двухполостным гиперболоидом называется поверхность, кано­ническое (простейшее) уравнение которой имеет вид:

$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=-1.\; \; \; (15)$$

(рис.3). При а=Ь уравнение (15) определяет двухполостный ги­перболоид вращения.

4. Параболоиды
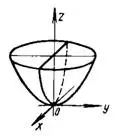
а) Эллиптическим параболоидом называется поверхность, кано­ническое (простейшее) уравнение которой имеет вид:

$$\frac{x^{2}}{p}+\frac{y^{2}}{q}=2z.\; \; \; (16)$$

(рис.4).
При p = q уравнение (16) определяет параболоид вращения

$$x^{2}+y^{2}=2pz.\; \; \; (16'))$$

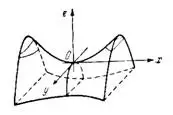
б) Гиперболическим параболоидом называется поверхность, ка­ноническое (простейшее) уравнение которой имеет вид:

$$\frac{x^{2}}{p}-\frac{y^{2}}{q}=2z.\; \; \; (17)$$

(рис.5).

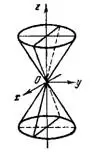
5. Конус второго порядка

$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}-\frac{z^{2}}{c^{2}}=0.\; \; \; (18)$$

(рис.6).
При а = b уравнение (18) определяет круго­вой конус

$$\frac{x^{2}+y^{2}}{a^{2}}-\frac{z^{2}}{c^{2}}=0.\; \; \; (18')$$

6. Цилиндры второго порядка
а) Эллиптическим цилиндром называется поверхность, каноническое уравнение которой имеет вид:

$$\frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1.\; \; \; (19)$$

(рис.7).

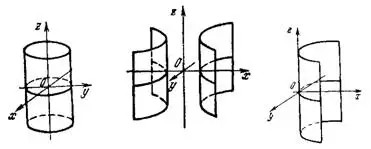
При а=b уравнение (19) определяет круговой цилиндр

$$x^{2}+y^{2}=a^{2}.\; \; \; (19'))$$

б) Гиперболическим цилиндром называется поверхность, кано­ническое уравнение которой имеет вид:

$$\frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1.\; \; \; (20)$$

(рис.8).
в) Параболическим цилиндром называется поверхность, канони­ческое уравнение которой имеет вид:

$$y^{2}=2px.\; \; \; (21)$$

(рис.9).
Общий метод исследования поверхностей по их уравнениям за­ключается в следующем:
1) находят сечения поверхности с каждой из трех координат­ных плоскостей;
2) находят сечения поверхности с плоскостями, параллельными координатным плоскостям;
3) анализируют кривые, полученные в результате сечений, и делают общее представление об исследуемой поверхности;
4) делают чертеж поверхности.