Цилиндрические и конические поверхности. Основные формулы

Цилиндрические и конические поверхности. Основные формулы

Поверхностью называется геометрическое место точек, коорди­наты которых удовлетворяют уравнению
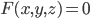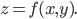$F(x,y,z)=0$ или $z=f(x,y).$   (1)
Линия в пространстве определяется совокупностью двух урав­нений

$$\left\{\begin{matrix} F_{1}(x;y;z)=0,\\ F_{2}(x;y;z)=0; \end{matrix}\right.\;\;\;(2)$$

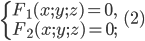
каждое из которых определяет некоторую поверхность.

Цилиндрические поверхности

Цилиндрической поверхностью называется поверхность, описы­ваемая прямой (образующей), параллельной данному направлению и пересекающей данную линию (направляющую).
Всякая цилиндрическая поверхность, образующие которой па­раллельны оси Oz (соответственно Оу, Ох), может быть представле­на уравнением
$F(x,y)=0$ или $y=f(x),$     (3)
(соответственно
$F(x,z)=0$ или $z=f(x)$; $F(y,z)=0$ или $z=f(y).$
На плоскости хОу уравнение $F(x,y)=0$ или $y=f(x),$ опреде­ляет линию, которая является направляющей этой цилиндрической поверхности.
Если уравнения направляющей искомой цилиндрической поверх­ности заданы в виде

$$\left\{\begin{matrix} F_{1}(x;y;z)=0,\\ F_{2}(x;y;z)=0; \end{matrix}\right.\;\;\;(4)$$

то уравнения образующих этой поверхности будут

$$\frac{X-x}{m}=\frac{Y-y}{n}=\frac{Z-z}{p},\;\;\;(5)$$

где (х,у,z) — точка, принадлежащая направляющей (4); m, n, p — направляющие коэффициенты образующих; X, Y, Z — текущие координаты цилиндрической поверхности. Исключая х, у, z из четырех уравнений (4) и (5), получим ис­комое уравнение цилиндрической поверхности.

Конические поверхности

Конической поверхностью называется поверхность, описываемая прямой, проходящей через данную точку — вершину конуса — и пере­секающей данную линию — направляющую конуса.
Если уравнения направляющей искомой конической поверхности заданы в виде

$$\left\{\begin{matrix} F_{1}(x;y;z)=0,\\ F_{2}(x;y;z)=0; \end{matrix}\right.\;\;\;(8)$$

то уравнения образующих этой поверхности будут:

$$\frac{X-x_{0}}{x-x_{0}}=\frac{Y-y_{0}}{y-y_{0}}=\frac{Z-z_{0}}{z-z_{0}},\;\;\;(9)$$

где (x;у;z) — точка, принадлежащая направляющей (8),
$(x_{0},y_{0},z_{0})$ — данная точка — вершина конуса;
Х; У; Z — текущие координаты конической поверхности.
Исключая x; у; z из четырех уравнений (8) и (9), получим иско­мое уравнение конической поверхности.